Η μεταφορά από ένα ουράνιο σώμα, σε άλλο.

 

Μια σφαίρα μάζας m=2kg ηρεμεί στη θέση Α και θέλουμε να την μεταφέρουμε στη θέση Β, του διπλανού σχήματος, όταν μεταξύ των δύο σημείων παρεμβάλλεται ένα βουναλάκι ύψους h₁=20m, ενώ η κατακόρυφη απόσταση των δύο σημείων είναι h₂=15m. Τριβές δεν υπάρχουν.

i)  Η μεταφορά μπορεί να γίνει με την επίδραση μιας μεταβλητής δύναμης F. Να υπολογιστεί το ελάχιστο έργο της δύναμης F, για την μεταφορά αυτή. Πόσο αυξήθηκε η μηχανική ενέργεια της σφαίρας κατά την παραπάνω μεταφορά;

ii) Εναλλακτικά μπορούμε να εκτοξεύσουμε τη σφαίρα, προσδίδοντάς της κατάλληλη αρχική ταχύτητα, η οποία θα της επιτρέψει να φτάσει στη θέση Β. Να υπολογιστεί η αρχική ταχύτητα εκτόξευσης, καθώς και η αύξηση της μηχανικής ενέργειας της σφαίρας, στην περίπτωση αυτή.

 iii) Ας θεωρήσουμε δύο ουράνια σώματα (δύο πλανήτες τους οποίους για τις ανάγκες του προβλήματος ας τους θεωρήσουμε ακίνητους) και μας ενδιαφέρει η μεταφορά ενός σώματος Σ μάζας m=2kg, από το σημείο Γ στην επιφάνεια του Χ, στο σημείο Δ, στην επιφάνεια του σώματος Υ. Στο διάγραμμα δίνεται ένα ποιοτικό διάγραμμα του δυναμικού του σύνθετου βαρυτικού πεδίου των δύο πλανητών, όπου οι τιμές των δυναμικών των σημείων Γ, Ο (το σημείο με το μέγιστο δυναμικό) και Δ: V_Γ= - 6∙10⁷ J/kg, V_Ο= - 1∙10⁷ J/kg και V_Δ= - 2∙10⁷ kg.

α) Ποια η ελάχιστη αρχική κινητική ενέργεια, που πρέπει να προσδώσουμε στο σώμα Σ για την μεταφορά του από τον πλανήτη Χ στον πλανήτη Υ;

β) Να βρεθεί η κινητική ενέργεια του σώματος Σ τη στιγμή που φτάνει στον πλανήτη Υ.

Απάντηση:

ή

Η μεταφορά από ένα ουράνιο σώμα, σε άλλο.

Η μεταφορά από ένα ουράνιο σώμα, σε άλλο.

Από ένα διάγραμμα δυναμικού…

 

Μια μικρή φορτισμένη σφαίρα, φέρει θετικό φορτίο (q>0) και κινείται ευθύγραμμα μέσα σε ένα ηλεκτροστατικό πεδίο, περνώντας από το σημείο Ο (στη θέση x=0) έχοντας κινητική ενέργειας Κ_ο=0,04J. Στο διπλανό διάγραμμα δίνεται το δυναμικό κατά μήκος της ευθείας x, πάνω στην οποία κινείται η σφαίρα.

i)  Η κινητική ενέργεια της σφαίρας τη στιγμή που διέρχεται από το σημείο Α, στη θέση x₁, έχει τιμή:

α) Κ₁=0,03J,    β) Κ₁=0,04J,   γ) Κ₁=0,05J.

ii)  Η κινητική ενέργεια της σφαίρας τη στιγμή που περνά από το σημείο Β, είναι ίση:

α) Κ₂=0,03J,     β) Κ₂=0,04J,      γ) Κ₂=0,05J.

iii) Ένας συμμαθητής σας υποστηρίζει ότι μεταξύ των σημείων Α και Β υπάρχει ένα σημείο, στο οποίο η ένταση του πεδίου είναι μηδενική. Να εξετάσετε αν έχει ή όχι δίκιο.

iv) Με βάση τις παραπάνω τιμές κινητικής ενέργειας που επιλέξατε, μπορείτε να υπολογίσετε το φορτίο q της σφαίρας;

v) Αν το δυναμικό στο σημείο Γ, έχει τιμή V_Γ=7.000V, να εξετάσετε αν η σφαίρα θα φτάσει ή όχι στο σημείο Γ.

Η κίνηση της σφαίρας γίνεται στο κενό και δεν δέχεται άλλες δυνάμεις, πέρα από την δύναμη του πεδίου.

Απάντηση:

 ή

 Από ένα διάγραμμα δυναμικού…

 Από ένα διάγραμμα δυναμικού…

Η κίνηση μιας φορτισμένης σφαίρας

 

Σε λείο μονωτικό οριζόντιο επίπεδο έχουν στερεωθεί δύο μικρές μεταλλικές σφαίρες Α και Β. Μια τρίτη μικρή σφαίρα Γ, μάζας m=0,02kg που φέρει φορτίο q=1μC κινείται ελεύθερα και ευθύγραμμα  όπως στο σχήμα, πάνω στην ευθεία ε, περνώντας από δύο θέσεις Ο και Κ με ταχύτητες μέτρων υ₁=4m/s και υ₂=6m/s.

i) Ποια πρόταση είναι σωστή:

α) Μόνο η σφαίρα Α είναι φορτισμένη.

β) Μόνο η σφαίρα Β είναι φορτισμένη.

γ) Και οι δυο σφαίρες Α και Β φέρουν φορτία.

δ) Καμιά από τις σφαίρες Α και Β δεν είναι φορτισμένη.

Να δικαιολογήσετε την επιλογή σας, καθορίζοντας και το είδος του φορτίου που έχει κάθε σφαίρα (αν έχει…).

ii) Να σχεδιάσετε στο σχήμα το διάνυσμα της επιτάχυνσης της σφαίρας Γ στη θέση Ο. Αν το μέτρο της επιτάχυνσης αυτής είναι α₁, τότε φτάνοντας στη θέση Κ θα έχει επιτάχυνση μέτρου:

α) α₂ < α₁,   β) α₂=α₁,   γ) α₂ >α₁.

Να δικαιολογήσετε την απάντησή σας.

iii) Να υπολογιστεί η κινητική ενέργεια της σφαίρας Γ στις θέσεις Ο και Κ, καθώς και το έργο της δύναμης από το ηλεκτρικό πεδίο, από το Ο στο Κ.

iv) Να βρεθεί η διαφορά δυναμικού V_ΟΚ μεταξύ των θέσεων Ο και Κ.

v)  Αν (ΑΟ)=(ΟΚ)=4,5cm, να υπολογιστεί το φορτίο της σφαίρας Α.

Δίνεται k=9∙10⁹Ν∙m²/C².

Απάντηση:

ή

 Η κίνηση μιας φορτισμένης σφαίρας

 Η κίνηση μιας φορτισμένης σφαίρας

Πληροφορίες από ένα διάγραμμα ταχύτητας.

 

Σε λείο οριζόντιο επίπεδο κινούνται ευθύγραμμα δυο ελαστικές σφαίρες Α και Β, με ίσες ακτίνες και κάποια στιγμή συγκρούονται κεντρικά. Στο διάγραμμα βλέπετε την μεταβολή της ταχύτητας της Α σφαίρας, σε συνάρτηση με το χρόνο.

i) Ποιο από τα παρακάτω σχήματα, δείχνει τις θέσεις και τις ταχύτητες των δύο σφαιρών πριν την κρούση;

 

ii) Ποιο από τα παρακάτω διαγράμματα θα μπορούσε να περιγράψει την ταχύτητα της Β  σφαίρας σε συνάρτηση με το χρόνο;

iii) Σχεδιάσαμε στο ίδιο διάγραμμα την ορμή κάθε σώματος σε συνάρτηση με το χρόνο. Ποιο από τα παρακάτω διαγράμματα πήραμε;

Να δικαιολογήσετε τις επιλογές σας

Απαντήσεις:

ή

Πληροφορίες από ένα διάγραμμα ταχύτητας.

Πληροφορίες από ένα διάγραμμα ταχύτητας.

Η ορμή και ο ρυθμός μεταβολής της ορμής.

Σε λείο οριζόντιο επίπεδο ηρεμεί ένα σώμα Α μάζας Μ=2kg. Ένα βλήμα μάζας m=0,1kg που κινείται οριζόντια με ταχύτητα υ₀= 100m/s, συγκρούεται με το σώμα Α, το διαπερνά σε χρόνο Δt=0,2s και εξέρχεται με ταχύτητα υ₁=40m/s.

i) Να υπολογιστεί η ταχύτητα του σώματος Α μετά την κρούση.

ii) Να βρεθεί  η μεταβολή της ορμής του βλήματος;

iii) Να υπολογιστεί η μέση δύναμη που δέχτηκε το βλήμα κατά το πέρασμά του μέσα από το σώμα Α, καθώς και ο μέσος ρυθμός μεταβολής της ορμής του σώματος Α στη διάρκεια της κρούσης.

Μια σφαίρα μάζας Μ=2kg είναι δεμένη στο άκρο νήματος μήκους ℓ=0,45m, το άλλο άκρο του οποίου είναι δεμένο στο ταβάνι. Φέρνουμε τη σφαίρα στη θέση Γ που δείχνει το σχήμα, όπου το νήμα είναι οριζόντιο και την αφήνουμε να κινηθεί.

iv) Να υπολογιστεί η ορμή και ο (στιγμιαίος) ρυθμός μεταβολής της ορμής της σφαίρας, τη στιγμή που το νήμα γίνεται κατακόρυφο.

Δίνεται g=10m/s².

Απάντηση:

ή

 Η ορμή και ο ρυθμός μεταβολής της ορμής.

 Η ορμή και ο ρυθμός μεταβολής της ορμής.

Η ορμή και οι μεταβολές της

Μια σφαίρα μάζας m=2kg κινείται σε λείο οριζόντιο επίπεδο, δεμένη στο άκρο νήματος μήκους ℓ=0,8m, διαγράφοντας κυκλική τροχιά κέντρου Ο, με γραμμική ταχύτητα σταθερού μέτρου υ=0,6m/s (το σχήμα σε κάτοψη).

i)  Να βρεθεί η ορμή και ο ρυθμός μεταβολής της ορμής (διεύθυνση, φορά και μέτρο) της σφαίρας στη θέση Α.

ii)  Σε πόσο χρόνο η σφαίρα θα φτάσει για πρώτη  φορά στη θέση Β, αντιδιαμετρική της θέσης Α; Να υπολογιστεί η μεταβολή της ορμής της σφαίρας στο παραπάνω χρονικό διάστημα.

iii) Μετά από λίγο η μπάλα φτάνει στη θέση Γ, όπου η ακτίνα ΟΓ είναι κάθετη στη διάμετρο ΑΒ. Να υπολογιστεί η μεταβολή της ορμής της σφαίρας μεταξύ των θέσεων Β και Γ.

iv) Να βρεθεί τέλος η μεταβολή της ορμής της σφαίρας, μεταξύ των θέσεων Γ και Δ, αν δίνεται για τη γωνία θ του σχήματος ημθ=0,6 και συνθ=0,8.

Απάντηση:

ή

Η ορμή και οι μεταβολές της

Η ορμή και οι μεταβολές της

Δυο υλικά σημεία σε ΟΚΚ.

Ένας δίσκος στρέφεται με το επίπεδό του κατακόρυφο, γύρω από σταθερό οριζόντιο άξονα ο οποίος περνά από το κέντρο του Ο, με σταθερή γωνιακή ταχύτητα ω, όπως στο σχήμα. Δυο μικρά σημειακά σώματα Σ₁ και Σ₂, της ίδιας μάζας, έχουν καρφωθεί στα σημεία Α και Β, όπου το Β βρίσκεται στο άκρο μιας ακτίνας R του δίσκου.

i)  Να σχεδιαστούν, πάνω στο σχήμα, οι ταχύτητες και οι επιταχύνσεις των σωμάτων Σ₁ και Σ₂.

ii) Μεγαλύτερη επιτάχυνση (κατά μέτρο) έχει:

α) Το σώμα Σ₁,   β) Το σώμα Σ₂,  γ) Έχουν επιταχύνσεις του ίδιου μέτρου.

iii) Να σχεδιάστε επίσης, σε ένα νέο σχήμα, την κεντρομόλο δύναμη που ασκείται σε κάθε σώμα.

 

iv) Αν τη στιγμή που δείχνει το σχήμα, η ακτίνα R είναι οριζόντια και η r κατακόρυφη:

α) Ποιο από τα  διανύσματα (1), (2), (3) παριστάνει την δύναμη F₁ που ασκεί ο δίσκος στο σώμα Σ₁;

β) Ποια η αντίστοιχη απάντηση για το διάνυσμα που παριστάνει την δύναμη F₂που ασκεί στο σώμα Σ₂ ο δίσκος;

v) Αν ω²=g/R, όπου g η επιτάχυνση της βαρύτητας και R η ακτίνα του δίσκου, να αποδείξετε ότι η δύναμη F₂ σχηματίζει γωνία 45° με την κατακόρυφη διεύθυνση.

Απάντηση:

ή

  Δυο υλικά σημεία σε ΟΚΚ.

  Δυο υλικά σημεία σε ΟΚΚ. 

Έργα και δυναμικές ενέργειες

1) Μια σφαίρα κρέμεται στο άκρο νήματος, όπως στο σχήμα. Σε μια στιγμή ασκείται πάνω της μια σταθερή κατακόρυφη δύναμη μέτρου F=4Ν και την επιταχύνει μέχρι να φτάσει στη θέση Β, όπου (ΑΒ)=0,5m, όπου η δύναμη καταργείται.

i) Πόση είναι η δυναμική ενέργεια της σφαίρας στη θέση Α;

ii) Πόση ενέργεια μεταφέρθηκε στη σφαίρα, μέσω του έργου της δύναμης F;

iii) Η κινητική ενέργεια της σφαίρας στη θέση Β είναι:
                            α) Κ_Β< 0,2J,   β) Κ_Β= 0,2J,    γ) Κ_Β> 0,2J 

iv) Αν η σφαίρα σταματά την άνοδό της στη θέση Γ, να βρεθεί η μεταβολή της δυναμικής ενέργειας της σφαίρας μεταξύ των θέσεων Α και Γ.

v) Αν η σφαίρα έχει μάζα 1kg, να υπολογιστεί η ταχύτητα της σφαίρας τη στιγμή που επιστρέφει στην αρχική της θέση Α (πριν τεντωθεί το νήμα…)

2) Σε λείο μονωτικό οριζόντιο επίπεδο έχει στερεωθεί ακλόνητα ένα σημειακό φορτίο Q. Μια μικρή φορτισμένη σφαίρα συνδέεται με το φορτίο Q  με αβαρές και μονωτικό νήμα, ενώ φέρει φορτίο q₁. Σε μια στιγμή ασκείται πάνω της μια σταθερή οριζόντια δύναμη μέτρου F₁=2Ν, η οποία την επιταχύνει μέχρι να φτάσει στη θέση Β, όπου (ΑΒ)=0,2m, όπου η δύναμη καταργείται.

i) Πόση είναι η δυναμική ηλεκτρική ενέργεια της φορτισμένης σφαίρας στη θέση Α;

ii) Πόση ενέργεια μεταφέρθηκε στη σφαίρα, μέσω του έργου της δύναμης F;

iii) Η κινητική ενέργεια της σφαίρας στη θέση Β είναι:

α) Κ_Β< 0,4J,   β) Κ_Β= 0,4J,    γ) Κ_Β> 0,4J

iv) Αν η σφαίρα σταματά την κίνησή της στη θέση Γ, να βρεθεί η μεταβολή της δυναμικής ενέργειας της σφαίρας μεταξύ των θέσεων Α και Γ.

v) Αν η σφαίρα έχει μάζα 0,2kg, να υπολογιστεί η ταχύτητά της, τη στιγμή που επιστρέφει στην αρχική της θέση Α (πριν τεντωθεί το νήμα…).

Απάντηση:

ή

 Έργα και δυναμικές ενέργειες

 Έργα και δυναμικές ενέργειες

Η μετατόπιση σε μία κυκλική κίνηση.

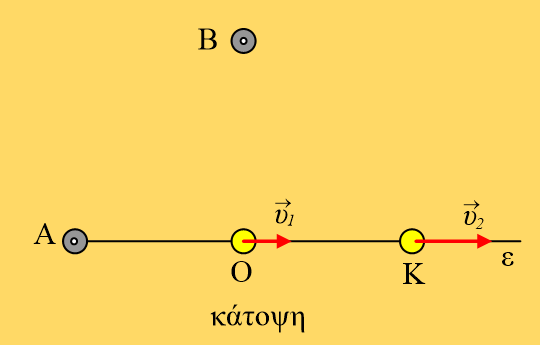
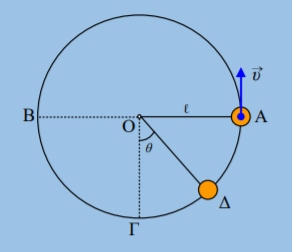
Από ένα σημείο Ο που το θεωρούμε ως αρχή των αξόνων, ξεκινάνε την χρονική στιγμή t₀ = 0, δύο κινητά Α και Β (θεωρείστε τα, σημειακά αντικείμενα) με ταχύτητες μέτρων υ₁ και υ₂ = 10π m/s. Το κινητό Α κινείται ευθύγραμμα και ομαλά κατά την θετική φορά του άξοναx′x, ενώ το κινητό Β εκτελεί ομαλή κυκλική κίνηση με το κέντρο του κύκλου που διαγράφει να βρίσκεται στη θέσηx₁ = 10 m. Τα δύο κινητά την χρονική t₁ = 5s έχουν ίσες μετατοπίσεις. Να βρεθούν:

α. Το μέτρο της ταχύτητας του κινητού Α.

β. Ο αριθμός των περιστροφών του κινητού Β μέχρι να αποκτήσουν ίσες μετατοπίσεις

Την χρονική στιγμή t₂= (2Ν + 1)Τ/4, όπου Τ η περίοδος της κυκλικής κίνησης του κινητού Β και Ν φυσικός αριθμός, η απόσταση των δύο κινητών είναι d = 26 m.

γ. Να βρεθεί η γωνία που έχει διαγράψει η επιβατική ακτίνα του κινητού Β.

Η συνέχεια εδώ.

Βολή στο κεκλιμένο. Η θεωρία …

Από κάποιο σημείο κεκλιμένου επιπέδου εκτοξεύουμε σώμα, με οριζόντια ταχύτητα υ₀, έτσι ώστε να προσγειωθεί σε κάποιο σημείο του κεκλιμένου επιπέδου. Η γωνία του κεκλιμένου επιπέδου είναι θ, όπως φαίνεται στο διπλανό σχήμα. Να βρεθούν:

α. Ποια είναι η μέγιστη απόσταση από το κεκλιμένο επίπεδο που βρίσκεται το σώμα κατά την διάρκεια της βολής.

β. Ποια χρονική στιγμή το σώμα βρίσκεται στην μέγιστη απόσταση από το κεκλιμένο επίπεδο.

γ. Ποια γωνία σχηματίζει η ταχύτητα υ με το κεκλιμένο επίπεδο όταν το σώμα απέχει την μέγιστη απόσταση από το κεκλιμένο επίπεδο.

Θεωρήστε γνωστό το ύψος Η μεταξύ του σημείου βολής και του σημείου πτώσης στο κεκλιμένο επίπεδο..

Η συνέχεια εδώ .

Η μετατόπιση στην οριζόντια βολή

Από το σημείο Ο, το οποίο βρίσκεται σε κάποιο ύψος από το έδαφος, εκτοξεύεται οριζόντια με αρχική ταχύτητα υ_ο, τη στιγμή t₀=0, μια μπάλα μάζας 0,5kg.  Την χρονική στιγμή t₁=2s, η μπάλα περνά από το σημείο Α, έχοντας μετατοπισθεί κατά 25m.

i)   Να βρεθεί η μεταβολή της ταχύτητας και η μεταβολή της κινητικής ενέργειας της μπάλας στο διάστημα 0-t₁.

ii) Να υπολογιστεί η κινητική ενέργεια της μπάλας στη θέση Α.

iii) Να βρεθεί η γωνία που σχηματίζει το διάνυσμα της μετατόπισης τη στιγμή t₁, με την οριζόντια διεύθυνση και να συγκριθεί με την αντίστοιχη γωνία που σχηματίζει το διάνυσμα της ταχύτητας της μπάλας στη θέση Α.

Η αντίσταση του αέρα θεωρείται αμελητέα, ενώ g=10m/s².

Απάντηση:

ή

 Η μετατόπιση στην οριζόντια βολή

 Η μετατόπιση στην οριζόντια βολή

Σχετικά με την ένταση ηλεκτρικού πεδίου

Στο σημείο Α, στο άκρο μιας ακτίνας ημικυκλίου με R=10cm, τοποθετούμε ένα σημειακό ηλεκτρικό φορτίο q₁=0,1 μC.

i)  Να σχεδιάσετε την ένταση του ηλεκτρικού πεδίου που δημιουργεί, στο κέντρο Ο του ημικυκλίου και να υπολογίσετε το μέτρο της.

ii)  Να βρεθεί το σημειακό ηλεκτρικό φορτίο q₂, το οποίο αν τοποθετήσουμε στη συνέχεια στο σημείο Β, θα έχει ως αποτέλεσμα το μηδενισμό της έντασης του ηλεκτρικού πεδίου στο κέντρο Ο.

iii) Το σημείο Γ του ημικυκλίου, απέχει 10cm από το Α. Να βρεθεί η ένταση του ηλεκτρικού πεδίου στο Γ, που οφείλεται στα φορτία q₁ και q₂.

Δίνεται k=9∙10⁹Ν∙m²/C².

Απάντηση:

ή

 Σχετικά με την ένταση ηλεκτρικού πεδίου

 Σχετικά με την ένταση ηλεκτρικού πεδίου

Βολή μες στην φρενίτιδα του ηλεκτρομαγνητισμού.

Σώμα Σ μάζας m = 0,2 kg, βάλλεται οριζόντια από ύψος h με ταχύτητα υ₀. Την στιγμή t₁ που η ταχύτητα του σώματος Σ σχηματίζει με την επιτάχυνση του γωνία θ = 30^ο ο ρυθμός μεταβολής της βαρυτική δυναμικής είναι ίσος με –60 J/s. Την στιγμή που η κινητική ενέργεια ισούται με την βαρυτική δυναμική ενέργεια το σώμα Σ απέχει από το έδαφος 70 m. Να βρεθούν:

α. Η χρονική στιγμή t₁

β. Η κινητική ενέργεια του σώματος Σ τη στιγμή της εκτόξευσης

γ. Το βεληνεκές της βολής

δ. Την μεταβολή της κινητικής ενέργειας στο τελευταίο δευτερόλεπτο της κίνησης.

Δίνεται g = 10 m/s². Οι αντιστάσεις από τον αέρα θεωρούνται αμελητέες. Επίπεδο μηδενικής δυναμικής ενέργειας θεωρούμε το έδαφος.

Λύση

Οι μπάλες φτάνουν ταυτόχρονα

Δυο όμοιες μπάλες εκτοξεύονται οριζόντια από δυο σημεία Α και Β τα οποία βρίσκονται σε ύψη h₁ και h₂, στο ίδιο κατακόρυφο επίπεδο. Οι μπάλες φτάνουν ταυτόχρονα στο έδαφος και στο ίδιο σημείο.

i)  Για τη χρονική στιγμή εκτόξευσης κάθε μπάλας ισχύει:

α) Πρώτα εκτοξεύθηκε η μπάλα στη θέση Α.

β) Πρώτα εκτοξεύθηκε η μπάλα στη θέση Β.

γ) Οι δυο μπάλες εκτοξεύθηκαν ταυτόχρονα.

ii) Αν h₂=4h₁ οι αρχικές ταχύτητες εκτόξευσης ικανοποιούν τη σχέση:

α) υ₁= ½ υ₂,   β) υ₁= υ₂,   γ) υ₁=2υ₂,   δ) υ₁= 4υ₂.

iii) Αν dΚ₁/dt ο τελικός ρυθμός μεταβολής της κινητικής ενέργειας της πρώτης μπάλας και dΚ₂/dt ο αντίστοιχος ρυθμός της δεύτερης μπάλας, ισχύει:

α) dΚ₁/dt< dΚ₂/dt   β)   dΚ₁/dt = dΚ₂/dt     γ) dΚ₁/dt > dΚ₂/dt  

Να δικαιολογήσετε τις απαντήσεις σας.

Η αντίσταση του αέρα θεωρείται αμελητέα.

Απάντηση:

ή

 Οι μπάλες φτάνουν ταυτόχρονα

 Οι μπάλες φτάνουν ταυτόχρονα

Κίνηση ηλεκτρικού φορτίου και ενέργειες

Μια ακίνητη μικρή φορτισμένη σφαίρα βρίσκεται στο σημείο Ο, έχοντας φορτίο Q=1μC. Στο σημείο Α, σε απόσταση r=1cm αφήνεται ένα σημειακό ηλεκτρικό φορτίο q, το οποίο δέχεται απωστική δύναμη μέτρου F=90Ν.

i)  Να υπολογιστεί το φορτίο q.

ii)  Να υπολογιστεί το έργο W₁ που παράγεται κατά την μετακίνηση του σημειακού φορτίου q, από το σημείο Α, σε άπειρη απόσταση. Τι ενεργειακές μετατροπές μετράει το έργο αυτό;

iii) Στο ηλεκτρικό κύκλωμα του σχήματος δίνονται Ε=18V, r=5Ω, R₁=35Ω και R₂=50Ω. 

α) Σε πόσο χρόνο διέρχεται φορτίο q από μια διατομή του κυκλώματος αυτού;

β) Πόση ενέργεια προσφέρει η πηγή σε φορτίο q, κατά την μετακίνησή του από τη θέση Β στη θέση Γ;

γ)  Να βρεθεί η αύξηση της δυναμικής ενέργειας του φορτίου q κατά την μετακίνησή του από το Β στο Γ. Να συγκρίνετε το αποτέλεσμα αυτό με το αποτέλεσμα του προηγούμενου ερωτήματος.

δ) Πόση ενέργεια μεταφέρει το παραπάνω φορτίο στον αντιστάτη με αντίσταση R₂;

Απάντηση:

ή

 Κίνηση ηλεκτρικού φορτίου και ενέργειες

Κίνηση ηλεκτρικού φορτίου και ενέργειες

Μια μικρή φορτισμένη σφαίρα σε ταλάντωση

Σε λείο μονωτικό οριζόντιο τραπέζι έχουν  στερεωθεί δυο μικρές φορτισμένες σφαίρες στα σημεία Α και Β, σε απόσταση (ΑΒ)=40cm, που φέρουν φορτία q₁=q₂=1μC.

Μεταξύ των δύο παραπάνω φορτισμένων σφαιρών, στη θέση Γ, όπου (ΑΓ)=10cm αφήνεται μια μικρή αγώγιμη σφαίρα Σ μάζας m=0,06g που φέρει φορτίο q=0,1μC.

i) Να υπολογιστεί η επιτάχυνση που θα αποκτήσει η σφαίρα Σ.

ii) Υποστηρίζεται ότι καθώς η σφαίρα κινείται προς τα δεξιά, η επιτάχυνσή της μειώνεται. Θεωρώντας τη σφαίρα στη θέση Δ, όπου (ΓΔ)=x, εξετάσετε αν αυτό είναι ή όχι σωστό.

iii) Να βρείτε την μέγιστη ταχύτητα που θα αποκτήσει η σφαίρα Σ.

Η κίνηση της σφαίρας Σ είναι μια ταλάντωση. Συνεπώς ένας μαθητής της Β΄ τάξης που εδώ και καιρό μελετάει την ύλη της Γ΄ τάξης αδιαφορώντας για το μάθημα της Β΄ τάξης (αφού του είναι «άχρηστο»), θα μπορούσε να εξετάσει αν η ταλάντωση αυτή είναι μια απλή αρμονική ταλάντωση. Αλλά ας δοκιμάσουμε κάτι πιο εύκολο. Μόνο λοιπόν για τους μαθητές που έχουν διδαχτεί (ιδιωτικά) ταλαντώσεις:

iv) Να βρεθεί η μέγιστη δυναμική ενέργεια ταλάντωσης και να αποδειχθεί ότι είναι ίση με την μέγιστη κινητική ενέργεια της σφαίρας Σ.

Δίνεται Κ_c=9∙10⁹ Ν∙m²/C².

Απάντηση:

ή

 Μια μικρή φορτισμένη σφαίρα σε ταλάντωση

Μια μικρή φορτισμένη σφαίρα σε ταλάντωση

Διαγώνισμα στο Ηλεκτρικό ρεύμα 2019

 

Στο διπλανό κύκλωμα οι αντιστάσεις των αντιστατών είναι: R₁ = 10 Ω , R₂ = 6 Ω , R₃ = 6 Ω , R₄ = 3 Ω και η πηγή με ηλεκτρεγερτική δύναμη E, έχει εσωτερική αντίσταση r. Οι αγωγοί σύνδεσης έχουν αμελητέα αντίσταση. Αρχικά ο διακόπτης είναι ανοικτός. Να υπολογίσετε: 

Γ1. Το λόγο των ισχύων P₃/P₄ που δαπανούν οι αντιστάτες R₃ και R₄ αντίστοιχα.

Γ2. Την ΗΕΔ της πηγής και την εσωτερική της αντίσταση r.

 Γ3. Τις εντάσεις των ηλεκτρικών ρευμάτων Ι και Ι₃, Ι₄ που διαρρέουν τους αντιστάτες R₃ και R₄ αντίστοιχα.  

Γ4. Το ποσοστό μεταβολής της ισχύος που δαπανά ο αντιστάτης R₂, αν κλείσουμε τον διακόπτη δ.

Η συνέχεια εδώ.

Η γεννήτρια και η ισχύς της σε διάφορες περιπτώσεις

Για το κύκλωμα του  διπλανού σχήματος δίνονται ότι η πηγή έχει ΗΕΔ Ε=20V και εσωτερική αντίσταση r=2Ω, ενώ οι αντιστάτες έχουν αντιστάσεις R₁=8Ω και R₂=4,8Ω.

i)  Να υπολογιστεί η ένταση του ρεύματος που  διαρρέει την πηγή, καθώς και ο ρυθμός με τον οποίο η πηγή παρέχει ενέργεια στο κύκλωμα.

ii)  Να βρεθεί η ισχύς της πηγής, όταν  συνδέσουμε τα σημεία Α και Β με ένα  σύρμα μηδενικής αντίστασης.

iii) Αφαιρούμε το παραπάνω σύρμα και συνδέουμε μεταξύ των σημείων Α και Β:

α) Ένα ιδανικό αμπερόμετρο,   β) ένα ιδανικό βολτόμετρο.

Να βρεθούν οι ενδείξεις των δύο οργάνων, καθώς και η πολική τάση της πηγής, σε κάθε περίπτωση.

Απάντηση:

ή

 Η γεννήτρια και η ισχύς της σε διάφορες περιπτώσεις

Η γεννήτρια και η ισχύς της σε διάφορες περιπτώσεις

Τρεις μεταβολές αερίων

Να αντιστοιχίσετε τις μεταβολές του παραπάνω σχήματος με τις τιμές της θερμότητας που ανταλλάσσει και του έργου που παράγει το αέριο, σε κάθε μεταβολή. Για κάθε μεταβολή να συμπληρώσετε τις τιμές για την μεταβολή της εσωτερικής ενέργειας του αερίου, στην τελευταία στήλη.

Ας σημειωθεί ότι στο σχήμα υπάρχει μια ισόθερμη και μια αδιαβατική μεταβολή.

Να δικαιολογήσετε τις απαντήσεις σας.

Απάντηση:

ή

  Τρεις μεταβολές αερίων

Τρεις μεταβολές αερίων