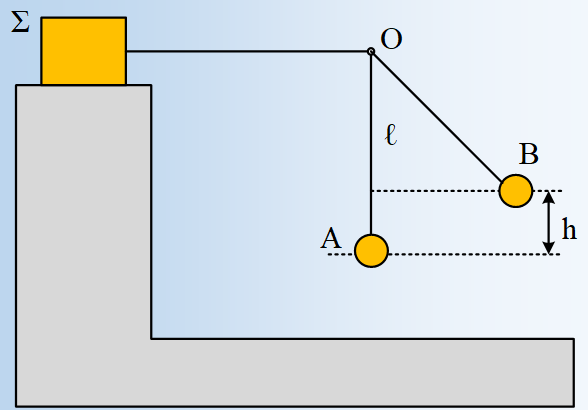
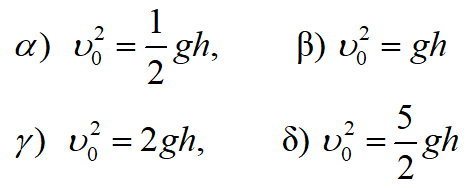Η σφαίρα του σχήματος, μάζας m1=3kg, ισορροπεί δεμένη στο άκρο μη ελαστικού κατακόρυφου νήματος μήκους ℓ=2m, το άλλο άκρο του οποίου έχει δεθεί σε σταθερό σημείο Ο, σε επαφή με σώμα Σ, μάζας m2=1kg, το οποίο παρουσιάζει με το οριζόντιο επίπεδο συντελεστή τριβής μ=0,3. Εκτρέπουμε τη σφαίρα, φέρνοντάς την στη θέση Α, όπου το νήμα σχηματίζει με την κατακόρυφη γωνία φ (ημφ=0,8 και συνφ=0,6) και την αφήνουμε να κινηθεί.
i) Ποια η αρχική επιτάχυνση της σφαίρας στη θέση Α, μόλις αφεθεί να κινηθεί;
ii) Να βρεθεί η ορμή και ο ρυθμός μεταβολής της ορμής της σφαίρας, τη στιγμή που το νήμα γίνεται κατακόρυφο, ελάχιστα πριν την σύγκρουσή της με το σώμα Σ.
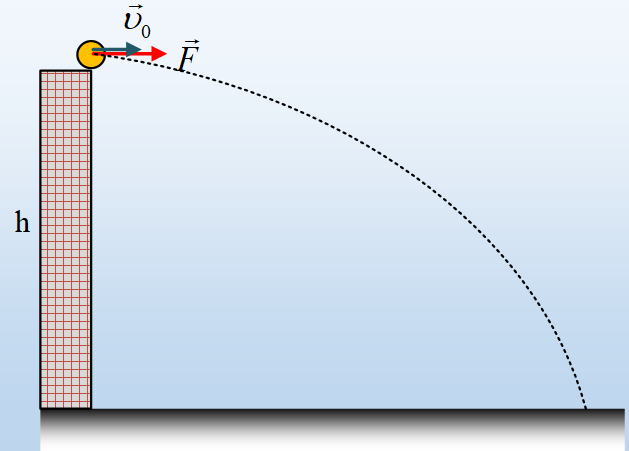
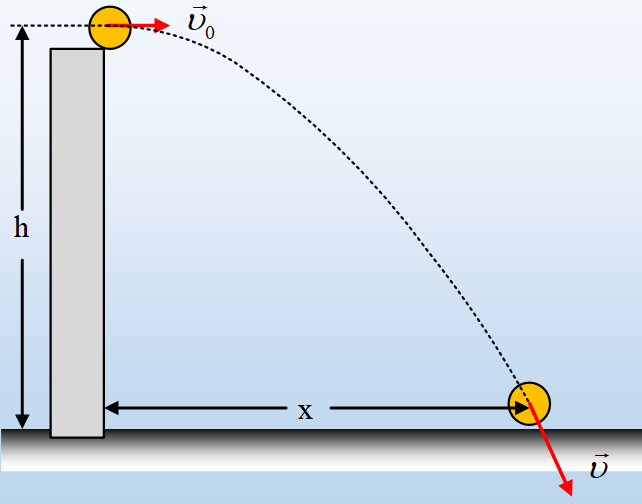
iii) Αν το σώμα Σ, μετά την κρούση διανύει απόσταση 6m στο οριζόντιο επίπεδο, μέχρι να σταματήσει, να βρεθεί η ενέργεια που κέρδισε στη διάρκεια της κρούσης.
iv) Η σφαίρα μετά την κρούση, θα εκτραπεί προς τα δεξιά ή προς τα αριστερά; Ποιο το μέγιστο ύψος στο οποίο θα φτάσει;
v) Κατά την παραπάνω κρούση μεταξύ των δύο σωμάτων είχαμε απώλεια μηχανικής ενέργειας ή όχι;
g=10m/s2.
ή