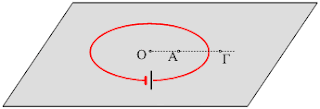
Ένα πλαίσιο σε δύο πεδία

Ένα τετράγωνο μεταλλικό πλαίσιο πλευράς α=1m και αντίστασης R=3Ω,  κινείται οριζόντια σε χώρο που υπάρχουν δύο κατακόρυφα ομογενή μαγνητικά πεδία, κάθετα στις δυναμικές γραμμές, όπως στο σχήμα, όπου Β₁=1Τ και Β₂=2Τ. Το πλαίσιο κινείται με σταθερή ταχύτητα υ=5m/s, με την επίδραση μιας οριζόντιας εξωτερικής δύναμης F.

Για τη θέση που φαίνεται στο σχήμα να βρεθούν:

i)  Η ένταση του ρεύματος που διαρρέει το πλαίσιο.

ii) Το μέτρο της εξωτερικής δύναμης F.

iii)  Οι τάσεις V_ΚΛ και V_ΝΜ.

Απάντηση:

Ερωτήσεις Ηλεκτρομαγνητισμού.

1)  Στο επίπεδο της σελίδας έχουμε ένα ορθογώνιο τρίγωνο ΚΛΜ. Από τις κορυφές Λ και Μ και κάθετα στο επίπεδο του τριγώνου διέρχονται δύο ευθύγραμμοι ρευματοφόροι αγωγοί που διαρρέονται από ρεύματα Ι₁=Ι₂, όπως στο σχήμα.

 

i)  Να σχεδιάστε την ένταση του μαγνητικού πεδίου στην κορυφή Κ.

ii) Πού είναι μεγαλύτερη η ένταση του πεδίου  στην κορυφή Κ ή στο μέσον O της ΛΜ;

2)  Σε οριζόντιο επίπεδο βρίσκεται ένας κυκλικός αγωγός που διαρρέεται από ρεύμα.

 i)   Να σχεδιάστε την ένταση του μαγνητικού πεδίου στα σημεία Ο, Α και Γ όπου Ο το κέντρο του κυκλικού αγωγού.

ii) Η ένταση του πεδίου στο σημείο Α είναι:

α) κατακόρυφη,   β) οριζόντια,   γ)  πλάγια.

iii) Για το μέτρο της έντασης στα σημεία Α και Γ ισχύει:

α) Β_Α<Β_Γ,                 β) Β_Α=Β_Γ,        γ) Β_Α>Β_Γ.

Απάντηση

Επαγωγή και πηγή.

Ο α­γω­γός ΑΓ έ­χει μή­κος 1m μάζα 2kg και α­ντί­στα­ση 3Ω και αφήνεται να κινηθεί ό­πως στο σχή­μα υ­πό την ε­πί­δρα­ση της στα­θε­ρής δύ­να­μης F =20Ν. Αν Β=2Τ και η πηγή έχει ΗΕΔ Ε=20V και εσωτερική αντίσταση r=1Ω.

i)  Ποια η αρχική επιτάχυνση που αποκτά ο αγωγός;

ii)  Μετά από λίγο ο αγωγός έχει ταχύτητα 4m/s. Για τη στιγμή αυτή:

α)  Ποια η ένταση του ρεύματος που διαρρέει το κύκλωμα;

β) Βρείτε την ισχύ της δύναμης F, την ισχύ της δύναμης Laplace και τον ρυθμό με τον οποίο αυξάνεται η κινητική ενέργεια της ράβδου.

γ) Να βρείτε την ισχύ της γεννήτριας, την ισχύ της ΗΕΔ από επαγωγή και την ισχύ που μετατρέπεται σε θερμότητα στο κύκλωμα.

Να σχολιάστε τα αποτελέσματα.

Απάντηση

Μαγνητική Ροή και επαγωγή.

Αφήνουμε τον αγωγό KΛ μάζας 1kg, μήκους L=1m και αντίστασης r=1Ω για t=0 να κινηθεί κατακόρυφα, από την οριζόντια θέση ΑΓ, όπως στο σχήμα, όπου R=3Ω και Β=2Τ. Μετά από χρόνο t₁ ο αγωγός έχει κατέλθει κατά y=2m και έχει αποκτήσει ταχύτητα υ₁=5m/s.

i) Για τη στιγμή t₁, να βρεθούν:

 α)  Η μαγνητική ροή που διέρχεται από το σχηματιζόμενο πλαίσιο ΑΓΚΛ, καθώς και ο ρυθμός μεταβολής της ροής. Θεωρείστε ότι η κάθετη στο πλαίσιο έχει την κατεύθυνση των δυναμικών γραμμών.

β)   Η επιτάχυνση του αγωγού ΑΓ.

ii)  Πόση θερμότητα αναπτύχθηκε στο κύκλωμα από 0-t₁.

iii)  Υπολογίστε το συνολικό φορτίο που μετακινήθηκε στο κύκλωμα από 0-t₁.

Δίνεται:    g=10m/s².

Απάντηση:

Κινήσεις φορτισμένων σωματιδίων λόγω ηλεκτρικών αλληλεπιδράσεων

Α) Για όσο χρονικό διάστημα αλληλεπιδρούν:

1) Τα μέτρα των ηλεκτρικών δυνάμεων αλληλεπίδρασης είναι ίσα

2) Το μέτρο του ρυθμού μεταβολής της ταχύτητας του σωματιδίου α είναι κάθε στιγμή ίσο με το μέτρο του ρυθμού μεταβολής της ταχύτητας του πυρήνα ασβεστίου

3) Το μέτρο του ρυθμού μεταβολής της ταχύτητας του σωματιδίου α είναι κάθε στιγμή δεκαπλάσιο από το μέτρο του ρυθμού μεταβολής της ταχύτητας του πυρήνα ασβεστίου

4) Η ολική ορμή του συστήματος των σωματιδίων διατηρείται σταθερή , αφού οι δυνάμεις ηλεκτρικής αλληλεπίδρασης είναι εσωτερικές δυνάμεις του συστήματος, το δε μέτρο της είναι ίσο με p_ολ =9m_aυ_ο

5) Η ολική ορμή του συστήματος των σωματιδίων διατηρείται σταθερή , αφού οι δυνάμεις ηλεκτρικής αλληλεπίδρασης είναι συντηρητικές, το δε μέτρο της είναι ίσο με p_ολ =11m_aυ_ο

6) Η μηχανική ενέργεια του συστήματος των δύο σωματιδίων διατηρείται σταθερή, αφού οι
δυνάμεις ηλεκτρικής αλληλεπίδρασης είναι συντηρητικές και είναι ίση...........

Συνέχεια

Ηλεκτρική ενέργεια - Ηλεκτρικές πηγές. Ένα Διαγώνισμα.

Δύο αντιστάτες R₁ και R₂ συνδέονται σε σειρά και στα άκρα τους συνδέεται μια πηγή ΗΕΔ Ε=4,5V και εσωτερικής αντίστασης r=1Ω. Ένας τρίτος αντιστάτης R₃ συνδέεται παράλληλα προς τους  δύο άλλους αντιστάτες R₁ και R₂. Στο κύκλωμα παρεμβάλουμε ένα αμπερόμετρο που μετρά το ρεύμα που διαρρέει τον αντιστάτη R₁ και ένα βολτόμετρο που μετρά την πολική τάση της πηγής.

i)   Να σχεδιάστε το κύκλωμα

ii)  Η ένδειξη του βολτομέτρου μπορεί να είναι:

α)  5V                   β)  4,5V                  γ)  4V

iii)  Το ρεύμα βραχυκύκλωσης  αυτής της πηγής θα είναι:

α)  4Α                   β)  4,5 Α                 γ)  45 Α

Να δικαιολογήσετε τις απαντήσεις σας.

Δείτε όλο το διαγώνισμα από εδώ.

Κίνηση σε ανομοιογενές και ομογενές ηλεκτρικό πεδίο

Σημειακό φορτίο q = - 10^-8C και μάζας m = 10^-6 Kg , αφήνεται ελεύθερο στη θέση Δ, σε απόσταση d = 2m από ακλόνητο σημειακό φορτίο Q = - 4·10^-8C, που έχει τοποθετηθεί στη θέση Γ. Το φορτίο Q βρίσκεται σε πολύ μεγάλη απόσταση από τον οπλισμό Α ενός πυκνωτή όπως φαίνεται στο παρακάτω σχήμα, στον οποίο έχει δημιουργηθεί ομογενές ηλεκτρικό πεδίο (Ο.Η.Π.) έντασης μέτρου Ε = 30 N/C, μεταξύ των οπλισμών του Α και Β. Το φορτίο q εισέρχεται από ένα σημείο Ο στον πυκνωτή και μόλις που φτάνει στον οπλισμό Β.
i.Να σχεδιάσετε τις δυναμικές γραμμές του Ο.Η.Πεδίου.
ii. Να βρείτε την τάση V μεταξύ των οπλισμών του πυκωτή.
iii. Να υπολογίσετε ...............................................

Η συνέχεια από ΕΔΩ

Κινούμενος αγωγός υπό γωνία σε ΟΜΠ.

Διδάσκουμε επαγωγή και ο τίτλος της παραγράφου λέει: «Ευθύγραμμος αγωγός κινούμενος σε ομογενές μαγνητικό πεδίο». Εκεί όμως ο αγωγός κινείται με ταχύτητα κάθετη στο μήκος του. Και αν η ταχύτητα σχηματίζει γωνία με τον αγωγό; Ή αν η γωνία αυτή είναι 90°; Αλλά και τι συμβαίνει με τη δύναμη Laplace που ασκείται στον αγωγό, αν υπάρχει κλειστό κύκλωμα; Είναι αντίθετη της ταχύτητας ή είναι κάθετη στον αγωγό;

Ένα βήμα παραπέρα. Και αν ο αγωγός δεν είναι ευθύγραμμος; Δεν αναπτύσσεται ΗΕΔ από επαγωγή; Δεν μπορούμε να την βρούμε; Μήπως μπορούμε να την υπολογίσουμε, αντικαθιστώντας τον με ένα ευθύγραμμο αγωγό; Στα ερωτήματα αυτά προσπαθεί να απαντήσει η παρακάτω άσκηση, η οποία προφανώς «θεωρείται δύσκολη» και έχουμε πάψει να την διδάσκουμε εδώ και κάποια χρόνια…

………………………………………………………………………………

Σε λείο οριζόντιο επίπεδο κινείται ένα τριγωνικό αγώγιμο πλαίσιο ΑΒΓ με αντίσταση R=0,2Ω και γωνία κορυφής Γ, τέτοια που ημθ=0,6 και συνθ=0,8. Σε μια στιγμή t₀=0 εισέρχεται σε ένα κατακόρυφο ομογενές μαγνητικό πεδίο έντασης Β=0,5Τ. Για τη στιγμή που φαίνεται στο σχήμα, όπου στο μαγνητικό πεδίο έχει εισέλθει τμήμα (ΓΔ)=0,4m, ο αγωγός έχει ταχύτητα υ=4m/s, παράλληλη στην πλευρά ΑΓ, ζητούνται:

i)    Η ΗΕΔ από επαγωγή που αναπτύσσεται σε κάθε πλευρά του πλαισίου.

ii)  Ο ρυθμός αύξησης της μαγνητικής ροής που διέρχεται από το πλαίσιο.

iii)  Η ένταση του ρεύματος που διαρρέει το πλαίσιο.

iv)  Η δύναμη Laplace που δέχεται κάθε πλευρά του πλαισίου από το μαγνητικό πεδίο.

v)  Η ηλεκτρική ισχύς που εμφανίζεται στο πλαίσιο και ο ρυθμός μεταβολής της κινητικής του ενέργειας.

Απάντηση:

Ηλεκτρικό πεδίο. Ένα test

2. Το φορτίο Q=-10μC του διπλανού σχήματος είναι ακλόνητο στην κορυφή του κεκλιμένου επιπέδου. Το φορτίο q=-1μC αφήνεται ελεύθερο να κινηθεί στη θέση Β που απέχει απόσταση ΑΒ=2m από το  A και στην οποία έχει βαρυτική δυναμική ενέργεια
U₁= 5 ∙10^-3 J.

 η συνέχεια και οι απαντήσεις από εδώ

Μαγνητικό πεδίο. Ένα test.

Ένα φορτισμένο σωματίδιο μάζας m και φορτίου  0,01μC εισέρχεται με ταχύτητα υ=200m/s σε μια περιοχή που υπάρχει ομογενές μαγνητικό πεδίο έντασης Β=0,2Τ, κάθετα στις δυναμικές γραμμές. Η τομή του μαγνητικού πεδίου είναι τετράγωνο πλευράς α=20cm και το σωματίδιο εισέρχεται στο πεδίο από το μέσον της πλευράς ΑΔ και εξέρχεται από την πλευρά ΓΔ, με ταχύτητα κάθετη στην ΓΔ, όπως στο σχήμα.

i)  Να σχεδιάστε την ένταση του μαγνητικού πεδίου και να υπολογίσετε το μέτρο της  δύναμης που ασκείται στο σωματίδιο. Να σχεδιάστε τη δύναμη που ασκείται στο σωματίδιο τη στιγμή της εξόδου από το πεδίο.

ii)  Να βρεθεί η ακτίνα της τροχιάς και η μάζα του σωματιδίου.

iii)  Ένα δεύτερο όμοιο σωματίδιο μπαίνει στο ίδιο μαγνητικό πεδίο από το μέσο της ΒΓ, όπως στο σχήμα, με ταχύτητα υ₁=400m/s. Να βρεθούν:

α) Το σημείο εξόδου του σωματιδίου αυτού από το πεδίο.

β)  Το χρονικό διάστημα που διαρκεί η κίνησή του μέσα στο πεδίο.

Μονάδες 5+5+6+4=20

 Δείτε τις απαντήσεις από εδώ.