Τρίτη 30 Οκτωβρίου 2018
Φυγοκέντρηση αίματος
Δευτέρα 29 Οκτωβρίου 2018
Δύναμη Coulomb…
Τρίτη 23 Οκτωβρίου 2018
Οι τάσεις των νημάτων.
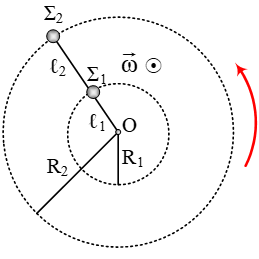 Τα
σημειακά σώματα Σ1 και Σ2 που
φαίνονται στην διπλανή εικόνα έχουν μάζες m1
= 0,2 kg και m2 =
0,4 kg αντίστοιχα. Τα δύο νήματα με μήκη ℓ1
και ℓ2 είναι αβαρή και μη εκτατά. Τα δύο σώματα περιστρέφονται με
σταθερή γωνιακή ταχύτητα, πάνω σε λείο οριζόντιο επίπεδο και η ακτίνα
περιστροφής του Σ2 είναι R2 = 30
cm. Το σώμα Σ1 σε όλη τη διάρκεια της
κυκλικής του κίνησης δέχεται δύο ακτινικές δυνάμεις με μέτρα 12 Ν και 14 Ν.
Τα
σημειακά σώματα Σ1 και Σ2 που
φαίνονται στην διπλανή εικόνα έχουν μάζες m1
= 0,2 kg και m2 =
0,4 kg αντίστοιχα. Τα δύο νήματα με μήκη ℓ1
και ℓ2 είναι αβαρή και μη εκτατά. Τα δύο σώματα περιστρέφονται με
σταθερή γωνιακή ταχύτητα, πάνω σε λείο οριζόντιο επίπεδο και η ακτίνα
περιστροφής του Σ2 είναι R2 = 30
cm. Το σώμα Σ1 σε όλη τη διάρκεια της
κυκλικής του κίνησης δέχεται δύο ακτινικές δυνάμεις με μέτρα 12 Ν και 14 Ν.
α. Να βρείτε τη δύναμη που δέχεται το Σ2 από το νήμα μήκους ℓ2 εξηγώντας αναλυτικά την απάντησή σας.
β. Να υπολογίσετε την κινητική ενέργεια του Σ2
γ. Να βρείτε τα μήκη των νημάτων.
Κάποια στιγμή το νήμα που συγκρατεί το Σ2 κόβεται και αυτό κινείται οριζόντια.
δ. Να βρείτε την οριζόντια απόσταση μεταξύ των Σ1 και Σ2 την στιγμή που οι ταχύτητες τους είναι κάθετες για πρώτη φορά.
Δίνεται π = 3,14.
Παρασκευή 19 Οκτωβρίου 2018
Μετά την κατηφόρα μια κυκλική κίνηση
Πέμπτη 11 Οκτωβρίου 2018
Η επιτάχυνση και ο ρόλος της.
1.
Ευθύγραμμη κίνηση:
Μια βολή στο ημικύκλιο.
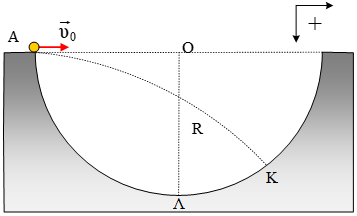 Από
ένα σημείο Α(0, 0), του οριζοντίου επιπέδου εκτοξεύουμε μικρή σφαίρα Σ, μάζας
m = 0,3 kg. Η σφαίρα
κάνει οριζόντια βολή σε ημικύκλιο ακτίνας R =
10√3 m.
Η μικρή σφαίρα χτυπά το ημικύκλιο στο σημείο Κ όπου η ακτίνα ΟΚ σχηματίζει με
την κατακόρυφη ακτίνα ΟΛ γωνία θ = 30ο. Να βρείτε:
Από
ένα σημείο Α(0, 0), του οριζοντίου επιπέδου εκτοξεύουμε μικρή σφαίρα Σ, μάζας
m = 0,3 kg. Η σφαίρα
κάνει οριζόντια βολή σε ημικύκλιο ακτίνας R =
10√3 m.
Η μικρή σφαίρα χτυπά το ημικύκλιο στο σημείο Κ όπου η ακτίνα ΟΚ σχηματίζει με
την κατακόρυφη ακτίνα ΟΛ γωνία θ = 30ο. Να βρείτε: Τρίτη 2 Οκτωβρίου 2018
Μια κυκλική κίνηση σε κατακόρυφο επίπεδο
Δευτέρα 1 Οκτωβρίου 2018
Δύο βολές ταυτόχρονα
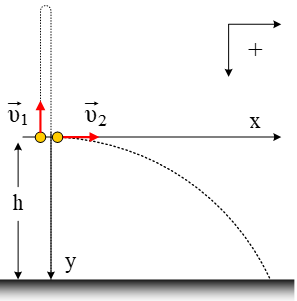 Δύο
σώματα Σ1 και Σ2 μάζας m = 0,2
kg, εκτοξεύονται ταυτόχρονα από το ίδιο σημείο, που
βρίσκεται σε ύψος h πάνω από την επιφάνεια της Γης. Το
μεν Σ1 κατακόρυφα προς τα πάνω, το δε Σ2 οριζόντια με την
ίδια κατά μέτρο ταχύτητα υ0. Τη στιγμή που το Σ2 φτάνει
στο έδαφος η απόσταση μεταξύ των δύο είναι η μέγιστη δυνατή, που μπορούν να
έχουν τα σημεία των τροχιών των δύο σωμάτων. Η απόσταση αυτή είναι
d = 40√2
m
Δύο
σώματα Σ1 και Σ2 μάζας m = 0,2
kg, εκτοξεύονται ταυτόχρονα από το ίδιο σημείο, που
βρίσκεται σε ύψος h πάνω από την επιφάνεια της Γης. Το
μεν Σ1 κατακόρυφα προς τα πάνω, το δε Σ2 οριζόντια με την
ίδια κατά μέτρο ταχύτητα υ0. Τη στιγμή που το Σ2 φτάνει
στο έδαφος η απόσταση μεταξύ των δύο είναι η μέγιστη δυνατή, που μπορούν να
έχουν τα σημεία των τροχιών των δύο σωμάτων. Η απόσταση αυτή είναι
d = 40√2
m







