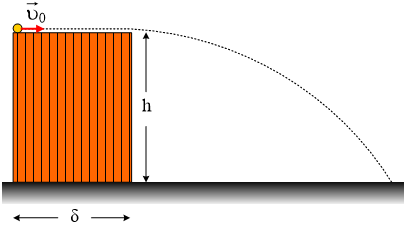
Τα διυλιστήρια
διαθέτουν μεγάλες κυλινδρικές δεξαμενές για την αποθήκευση των προϊόντων
πετρελαίου. Μία από αυτές τις δεξαμενές την έχουμε κάνει εργαστήριο πειραμάτων
για την μελέτη της οριζόντιας βολής. Κατά μήκος μίας διαμέτρου την χρονική
στιγμή
t0 = 0, από σημείο της περιφέρειας
εκτοξεύουμε σώμα μάζας
m = 0,2
kg,
με αρχική ταχύτητα μέτρου υ
0, προς το κέντρου του κύκλου. Την χρονική
στιγμή
t1 το σώμα φτάνει στο αντιδιαμετρικό
σημείο – από το σημείο εκτόξευσης – και στην συνέχεια εκτελεί οριζόντια βολή
φτάνοντας στο έδαφος την χρονική στιγμή
t2.
Η εξίσωση της ταχύτητας του σώματος κατά την διάρκεια της πτώσης δίνεται από την
σχέση
υ = √(400 + 100(t
- 2)2 S.
I.
για 2
s ≤
t ≤ 5
s. Να βρείτε:
α. το ύψος της δεξαμενής
β. την κινητική ενέργεια του σώματος την
στιγμή της εκτόξευσης
γ. τις εξισώσεις κίνησης για τον οριζόντιο
και κατακόρυφο άξονα και την εξίσωση της τροχιάς
δ. τον όγκο του πετρελαίου που μπορούμε να
αποθηκεύσουμε στην δεξαμενή, αν για λόγους ασφαλείας θα πρέπει να αφήσουμε 10%
αέρα μέσα.
ε. Σε ποιο
ύψος πάνω από το έδαφος η κινητική ενέργεια, είναι Κ = 2,25U
(κατά τη διάρκεια της πτώσης).
Δίνεται
g = 10 m/s2,
ο συντελεστής τριβής ολίσθησης σώματος δεξαμενής μ = 0,25, ο όγκος κυλίνδρου
V = πR2h,
όπου R η ακτίνα της βάσης και h
το ύψος. Ως αρχή των μετρήσεων (0, 0), θεωρούμε το σημείο εκτόξευσης,
θετική την φορά προς τα δεξιά του οριζοντίου άξονα και προς τα κάτω για τον
κατακόρυφο άξονα.
Οι αντιστάσεις
από τον αέρα θεωρούνται αμελητέες και επίπεδο μηδενικής δυναμικής ενέργειας
θεωρούμε το έδαφος. Το σώμα το θεωρούμε υλικό σημείο.


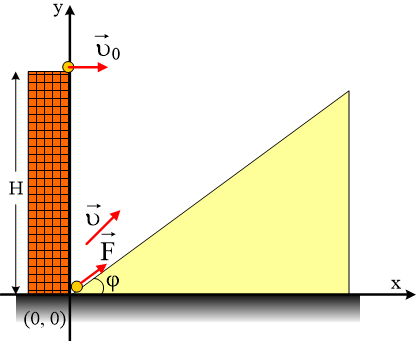 Από κτήριο
ύψους
Από κτήριο
ύψους 
 Τα διυλιστήρια
διαθέτουν μεγάλες κυλινδρικές δεξαμενές για την αποθήκευση των προϊόντων
πετρελαίου. Μία από αυτές τις δεξαμενές την έχουμε κάνει εργαστήριο πειραμάτων
για την μελέτη της οριζόντιας βολής. Κατά μήκος μίας διαμέτρου την χρονική
στιγμή
Τα διυλιστήρια
διαθέτουν μεγάλες κυλινδρικές δεξαμενές για την αποθήκευση των προϊόντων
πετρελαίου. Μία από αυτές τις δεξαμενές την έχουμε κάνει εργαστήριο πειραμάτων
για την μελέτη της οριζόντιας βολής. Κατά μήκος μίας διαμέτρου την χρονική
στιγμή 
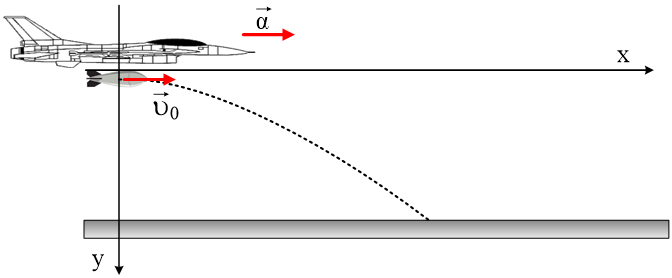 Ένα μαχητικό αεροπλάνο μάζας Μ = 40000
Ένα μαχητικό αεροπλάνο μάζας Μ = 40000