Ασκήσεις Φυσικής Β΄ Λυκείου Γ.Π.

Στο παρακάτω αρχείο περιλαμβάνονται οι ασκήσεις για τη Φυσική γενικής παιδείας Β΄ Λυκείου.

Πρόκειται συνολικά για 103 Ασκήσεις που δημοσιεύτηκαν τα προηγούμενα χρόνια στο δίκτυό μας.

 Ασκήσεις Φυσικής Β΄ Λυκείου Γ.Π.

 Ασκήσεις Φυσικής Β΄ Λυκείου Γ.Π.

Κυκλική κίνηση και ορμή

  

Σε ένα αμαξίδιο έχει προσαρμοσθεί κατάλληλο στήριγμα, από σημείο Ο του οποίου κρέμεται, μέσω νήματος μήκους l=1m, μια σφαίρα μάζας m=1kg. Σε μια στιγμή η σφαίρα δέχεται στιγμιαίο κτύπημα, με αποτέλεσμα να αποκτήσει οριζόντια ταχύτητα υ₀. Συγκρατώντας ακίνητο το αμαξίδιο, η σφαίρα ανέρχεται μέχρι τη θέση Β, σε ύψος h=0,8m, πριν κινηθεί ξανά προς τα κάτω.

i)  Να υπολογισθεί η αρχική ορμή της σφαίρας (αμέσως μετά το κτύπημα), καθώς και ο αντίστοιχος ρυθμός μεταβολής της ορμής της.

ii) Να βρεθεί η τάση του νήματος, καθώς και η στιγμιαία επιτάχυνση της σφαίρας, στη θέση Β.

iii) Επαναλαμβάνουμε το πείραμα, η σφαίρα αποκτά την ίδια αρχική ταχύτητα υ₀, μετά το κτύπημα, αλλά τώρα αφήνουμε το αμαξίδιο ελεύθερο να κινηθεί, στο λείο οριζόντιο επίπεδο. Αν η μέγιστη ταχύτητα που αποκτά το αμαξίδιο, μέχρι να σταματήσει η άνοδος της σφαίρας, έχει μέτρο υ_κ=1m/s, ενώ το νήμα παραμένει διαρκώς τεντωμένο, να βρεθούν:

α) Η συνολική μάζα Μ αμαξιδίου- στηρίγματος.

β) Το μέγιστο ύψος h΄ στο οποίο θα φτάσει η σφαίρα.

Απάντηση:

ή

 Κυκλική κίνηση και ορμή

 Κυκλική κίνηση και ορμή

Ασκήσεις Φυσικής Β΄ Τάξης, Προσανατολισμού

Δίνω παρακάτω ένα αρχείο pdf, με όλες τις ασκήσεις της Β΄ τάξης Λυκείου προσανατολισμού, που έχω δημοσιεύσει και στο δίκτυο και πριν στο Blogspot.

Πρόκειται για 310 ασκήσεις- ερωτήσεις … μέχρι τις φετινές εξετάσεις.

Φυσική Προσανατολισμού Β΄ Τάξη.

ή

 Φυσική Προσανατολισμού Β΄ Τάξη.

Η ορμή για κίνηση πάνω σε βάση

 

Ένα μικρό σώμα Σ μάζας m ηρεμεί πάνω σε μια βάση, στη θέση Α, όπως στο σχήμα. Η βάση έχει μάζα Μ=3m και βρίσκεται σε λείο οριζόντιο επίπεδο. Σε μια στιγμή το σώμα Σ δέχεται στιγμιαίο κτύπημα, με αποτέλεσμα να αποκτήσει οριζόντια ταχύτητα υ₀ και να κινηθεί πάνω στη βάση και μετά από λίγο αρχίζει να ανέρχεται φτάνοντας μέχρι την θέση Β του σχήματος, πριν κινηθεί ξανά προς τα κάτω. Τριβές μεταξύ του σώματος Σ και της βάσης, δεν υπάρχουν.

i) Στη διάρκεια της μετακίνησης του Σ από το Α στο Β, η βάση παραμένει ή όχι ακίνητη;

ii) Στη θέση Β, όπου το Σ σταματά να κινείται προς τα πάνω κατά μήκος της βάσης, έχει ταχύτητα:

α) μηδενική.

β) οριζόντια προς τα δεξιά.

γ) οριζόντια προς τα αριστερά.

iii) Να υπολογιστεί η μέγιστη ταχύτητα της βάσης, μέχρι να φτάσει το σώμα Σ στη θέση Β.

iv) Κατά τη διάρκεια της κίνησης του σώματος Σ από τη θέση Α στη θέση Γ, η ορμή του συστήματος σώμα Σ-βάση, παραμένει σταθερή ή όχι;

Να δικαιολογήσετε αναλυτικά τις απαντήσεις σας.

Απάντηση:

ή

  Η  ορμή για κίνηση πάνω σε βάση

  Η  ορμή για κίνηση πάνω σε βάση

Συνδέοντας και μεταβάλλοντας μια αντίσταση

 

Στο διπλανό κύκλωμα ο διακόπτης είναι ανοικτός και το αμπερόμετρο ιδανικό. Δίνονται Ε=12V, r=3Ω και R₁=5Ω.

i)  Ποια η ένδειξη του αμπερομέτρου;

Κλείνουμε το διακόπτη με αποτέλεσμα να παρεμβάλουμε στο κύκλωμα μια μεταβλητή αντίσταση R.

ii) Η ένδειξη του αμπερομέτρου, θα αυξηθεί, θα μειωθεί ή θα παραμείνει σταθερή; Να δικαιολογήσετε την απάντησή σας.

iii) Μεταβάλλοντας την τιμή της αντίστασης R, παίρνουμε πειραματικές τιμές για την ένταση του ρεύματος που διαρρέει την πηγή και κατασκευάσαμε το διπλανό διάγραμμα Ι=f(R).

α) Ποια η τιμή της έντασης (β) όταν R=7,5Ω;

β) Να βρεθούν οι τιμές α και γ της έντασης.

Απάντηση:

ή

  Συνδέοντας και μεταβάλλοντας μια αντίσταση
  Συνδέοντας και μεταβάλλοντας μια αντίσταση

Συμπίεση και αποσυμπίεση αερίου…

 

Σε δοχείο που κλείνεται με έμβολο περιέχονται Ν=12·10²³ μόρια Ηλίου, σε κατάσταση Α, με όγκο 20L και πίεση 3∙10⁵Ν/m². Συμπιέζουμε με σταθερή πίεση το αέριο μέχρι να αποκτήσει όγκο 8L (κατάσταση Β) και στη συνέχεια το αφήνουμε να εκτονωθεί ισόθερμα στον αρχικό του όγκο (κατάσταση Γ).  Ζητούνται:

i) Η απόλυτη θερμοκρασία του αερίου και η μέση κινητική ενέργεια των μορίων του στην κατάσταση Α.

ii) Η θερμοκρασία στην κατάσταση Β και η πίεση στην κατάσταση Γ.

iii) Να παραστήσετε τις παραπάνω μεταβολές σε άξονες p-V, p-Τ και V-Τ.

iv) Η ενεργός ταχύτητα των μορίων στην κατάσταση Α.

Δίνονται Ν_Α=6·10²³μόρια/mοℓ, R=8,314=25/3 J/mοℓ·Κ και η γραμμομοριακή μάζα Ηe Μ=4·10^-3kg/mοℓ.

Απάντηση:

ή

 Συμπίεση και αποσυμπίεση αερίου…

 Συμπίεση καιαποσυμπίεση αερίου…

Η ορμή και η ενέργεια σε ένα σύστημα.

 

Δυο σώματα Α και Β με μάζες m₁=10kg και m₂=20kg αντίστοιχα, είναι δεμένα στα άκρα ιδανικού ελατηρίου σταθεράς k=40Ν/m και ηρεμούν σε λείο οριζόντιο επίπεδο. Σε μια στιγμή t₀=0 ασκούμε στο Α σώμα μια σταθερή οριζόντια δύναμη μέτρου F=40Ν, όπως στο σχήμα, με αποτέλεσμα τα σώματα να κινηθούν και τη στιγμή  t₁=2s το σώμα Α να έχει ταχύτητα υ₁=1,6m/s, ενώ το ελατήριο έχει επιμήκυνση Δl=0,6m.

i) Ποιος ο αρχικός ρυθμός μεταβολής της ορμής κάθε σώματος;

ii) Να υπολογιστεί η ορμή του συστήματος των δύο σωμάτων τη χρονική στιγμή t₁.

iii) Να βρεθεί την παραπάνω στιγμή η ορμή και ο ρυθμός μεταβολής της ορμής κάθε σώματος.

iv)  Να υπολογιστεί η μετατόπιση του Α σώματος στο χρονικό διάστημα t₀ έως t₁.

Απάντηση:

ή

  Η ορμή και η ενέργεια σε ένα σύστημα.

  Η ορμή και η ενέργεια σε ένα σύστημα.

Μια κίνηση σε κυκλική τροχιά και μια κρούση

 

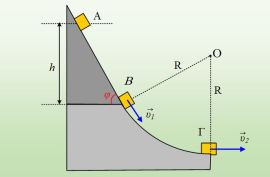
Μια σφαίρα μάζας 2kg είναι δεμένη στο άκρο αβαρούς και μη εκτατού νήματος μήκους l=1,25m, το άλλο άκρο του οποίου έχει δεθεί σε σταθερό σημείο Ο. Φέρνουμε τη σφαίρα στη θέση Α, ώστε το νήμα να γίνει οριζόντιο και την αφήνουμε να κινηθεί. Μόλις το νήμα γίνει κατακόρυφο, στη θέση Β, η σφαίρα συγκρούεται με έναν κατακόρυφο τοίχο, με αποτέλεσμα να επιστρέφει και να φτάνει μέχρι τη θέση Γ, η οποία βρίσκεται χαμηλότερα, σε κατακόρυφη απόσταση h=0,45m, από την αρχική θέση Α.

i) Να υπολογιστεί η ταχύτητα με την οποία η σφαίρα, φτάνει στην θέση Β (υπόδειξη: δουλέψτε ενεργειακά).

ii) Να βρεθεί η επιτάχυνση της σφαίρας στην αρχική θέση Α, μόλις αφεθεί να κινηθεί, καθώς και στη θέση Β, ελάχιστα πριν την κρούση με τον τοίχο. Ποια η τιμή της τάσης του νήματος στις δύο αυτές θέσεις;

iii) Να υπολογιστεί η ταχύτητα της σφαίρας αμέσως μετά την κρούση της με τον τοίχο.

iv) Να υπολογιστεί η μεταβολή της ορμής της σφαίρας που οφείλεται στην κρούση.

Δίνεται g=10m/s².

Απάντηση:

ή

  Μια κίνηση σε κυκλική τροχιά και μια κρούση

 Μια κίνηση σε κυκλική τροχιά και μια κρούση

Μελέτη και μετατροπές ενός κυκλώματος

 

Στο διπλανό κύκλωμα το ιδανικό αμπερόμετρο δείχνει ένδειξη Ι₁ =0,72 Α, ενώ γνωρίζουμε τις τιμές των δύο αντιστάσεων R₁=20Ω και R₂=80Ω και την Ηλεκτρεγερτική δύναμη της πηγής Ε=72V.

i)  Να υπολογιστεί η εσωτερική αντίσταση της πηγής και η πολική της τάση.

ii)  Στο παραπάνω κύκλωμα, παράλληλα προς τον αντιστάτη R₂, συνδέουμε ένα άλλο, με αντίσταση R₃=20Ω.

α) Να σχεδιάσετε το κύκλωμα και να υπολογίσετε την ολική εξωτερική αντίσταση.

β) Ποια η ένδειξη του αμπερομέτρου;

γ) Να συνδέσετε στο κύκλωμα ένα ιδανικό βολτόμετρο, το οποίο να μετρά την τάση στα άκρα του αντιστάτη R₂. Ποια η ένδειξή του;

iii) Να συνδέσετε δύο σημεία του παραπάνω κυκλώματος με ένα αγωγό χωρίς αντίσταση, έτσι ώστε το αμπερόμετρο να διαρρέεται από μέγιστο ρεύμα. Αφού σχεδιάσετε το κύκλωμα που προκύπτει να βρείτε τις ενδείξεις αμπερομέτρου και βολτομέτρου.

Απάντηση:

ή

 Μελέτη και μετατροπές ενός κυκλώματος

 Μελέτη και μετατροπές ενός κυκλώματος

Με αφορμή ένα δύσκολο πρόβλημα

Για το κύκλωμα του  διπλανού σχήματος δίνονται ότι τo βολτόμετρο με εσωτερική αντίσταση R_v=500Ω δείχνει ένδειξη V_v=V_ΒΕ = 50V, R₁=200Ω, R₂=500Ω, ενώ το ιδανικό αμπερόμετρο δείχνει ένδειξη Ι₂=0,3 Α.

i)  Να βρεθεί η τάση V_ΑΒ καθώς και η ένταση Ι₁ που διαρρέει τον κλάδο ΑΒ του κυκλώματος.

ii) Να βρεθούν οι εντάσεις των ρευμάτων που διαρρέουν τους δύο άλλους αντιστάτες και την πηγή τάσεως V.

iii) Αν R₃=250Ω να υπολογιστούν:

α) Η τιμή της αντίστασης R₄.

β) Η τάση V.

Απάντηση:

ή

 Με αφορμή ένα δύσκολο πρόβλημα

 Με αφορμή ένα δύσκολο πρόβλημα