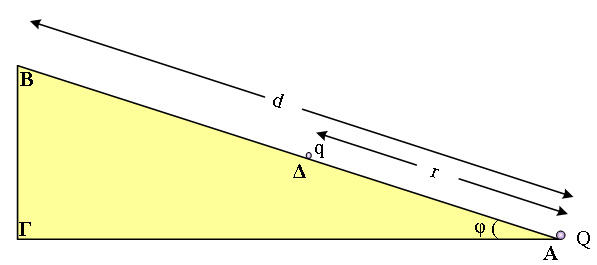
 Στη βάση λείου πλαγίου επιπέδου γωνίας φ = 30ο υπάρχει ακλόνητο σημειακό φορτίο Q = 10–3
C. Πάνω στο επίπεδο και σε απόσταση r = 30 cm από το φορτίο Q συγκρατείται σφαιρίδιο μάζας m = 0,1
kg και φορτίου q = 10–8 C όπως δείχνει το σχήμα.
Στη βάση λείου πλαγίου επιπέδου γωνίας φ = 30ο υπάρχει ακλόνητο σημειακό φορτίο Q = 10–3
C. Πάνω στο επίπεδο και σε απόσταση r = 30 cm από το φορτίο Q συγκρατείται σφαιρίδιο μάζας m = 0,1
kg και φορτίου q = 10–8 C όπως δείχνει το σχήμα. Τετάρτη 26 Φεβρουαρίου 2014
Κίνηση σε ανομοιογενές ηλεκτρικό πεδίο
 Στη βάση λείου πλαγίου επιπέδου γωνίας φ = 30ο υπάρχει ακλόνητο σημειακό φορτίο Q = 10–3
C. Πάνω στο επίπεδο και σε απόσταση r = 30 cm από το φορτίο Q συγκρατείται σφαιρίδιο μάζας m = 0,1
kg και φορτίου q = 10–8 C όπως δείχνει το σχήμα.
Στη βάση λείου πλαγίου επιπέδου γωνίας φ = 30ο υπάρχει ακλόνητο σημειακό φορτίο Q = 10–3
C. Πάνω στο επίπεδο και σε απόσταση r = 30 cm από το φορτίο Q συγκρατείται σφαιρίδιο μάζας m = 0,1
kg και φορτίου q = 10–8 C όπως δείχνει το σχήμα. Τρίτη 25 Φεβρουαρίου 2014
Μετά το ηλεκτρικό πεδίο συνεχίζει σε μαγνητικό!
Παρασκευή 21 Φεβρουαρίου 2014
Δύο πυκνωτές συνδέονται μέσω αντιστάτη.
Κυριακή 16 Φεβρουαρίου 2014
ΕΞΟΔΟΣ ΑΠΟ ΤΟ ΜΑΓΝΗΤΙΚΟ ΠΕΔΙΟ
Σάββατο 15 Φεβρουαρίου 2014
Κίνηση σε ομογενές και ανομοιογενές ηλεκτρικό πεδίο
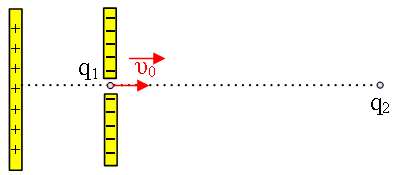 Σωματίδιο
μάζας m1 = 3·10–15kg και φορτίου q1 = +30 μC αφήνεται κοντά στον θετικό οπλισμό πυκνωτή
τάσης V = 1800 V και απόσταση οπλισμών d = 6 cm.
Το σωματίδιο εξέρχεται από τον πυκνωτή από μία μικρή οπή που υπάρχει στον αρνητικό οπλισμό. Σε μεγάλη απόσταση από την έξοδο από τον πυκνωτή και στην ίδια
ευθεία που κινείται το σωματίδιο m1 αφήνεται σωματίδιο q2, m2 = 2m1 ελεύθερο να κινηθεί. Να υπολογίσετε:
Σωματίδιο
μάζας m1 = 3·10–15kg και φορτίου q1 = +30 μC αφήνεται κοντά στον θετικό οπλισμό πυκνωτή
τάσης V = 1800 V και απόσταση οπλισμών d = 6 cm.
Το σωματίδιο εξέρχεται από τον πυκνωτή από μία μικρή οπή που υπάρχει στον αρνητικό οπλισμό. Σε μεγάλη απόσταση από την έξοδο από τον πυκνωτή και στην ίδια
ευθεία που κινείται το σωματίδιο m1 αφήνεται σωματίδιο q2, m2 = 2m1 ελεύθερο να κινηθεί. Να υπολογίσετε:Βρείτε το λάθος. Μια αδιαβατική μεταβολή.
Δευτέρα 3 Φεβρουαρίου 2014
Τρία φορτία σε αλληλεπίδραση και κυκλική κίνηση
Κυριακή 2 Φεβρουαρίου 2014
Κινήσεις σε ανομοιογενές ηλεκτρικό πεδίο
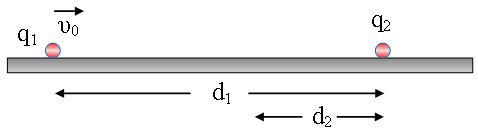
Σωματίδιο με μάζα m1 = 10–4kg και φορτίο q1 = 1 μC, εκτοξεύεται με ταχύτητα μέτρου υ0 την στιγμή η δυναμική ενέργεια εξαιτίας της αλληλεπίδρασης με ακλόνητο φορτίο q2 είναι ίση με U1 = 0,1 J, προς το φορτίο q2. Όταν μηδενίζεται ο ρυθμός μεταβολής της κινητικής ενέργειας του φορτίου q1 ο ρυθμός μεταβολής της ορμής έχει μέτρο dp/dt = 20 kg·m/s2 και απέχει από το q2 απόσταση d2 = 3 cm. Να βρείτε:
Α α. το μέτρο της αρχικής ταχύτητας εκτόξευσης υ0
β. το φορτίο q2 και την αρχική απόσταση d1
Β. Επαναλαμβάνουμε την ίδια διαδικασία αλλά αυτή την φορά αφήνουμε ελεύθερο το φορτίο q2 να κινηθεί.
γ. ποια η μέγιστη δυναμική ενέργεια τους;
δ. αν την στιγμή που πάψουν τα δύο φορτία να αλληλεπιδρούν η ταχύτητα του φορτίου q1 έχει μέτρο υ1 = 50 m/sκαι κατεύθυνση αντίθετη της αρχικής, να βρείτε το μέτρο της ταχύτητας του φορτίου q2.
Δίνονται η σταθερά του Coulomb Kc = 9·109N·m2/C2,m2 = 3m1.
Τριβές και κάθε είδους αντιστάσεις θεωρούνται αμελητέες.





