ΠΑΜΕ ΚΟΥΒΑ (ΧΩΡΙΣ ΝΑ ΠΑΙΞΟΥΜΕ ΣΤΟΙΧΗΜΑ)

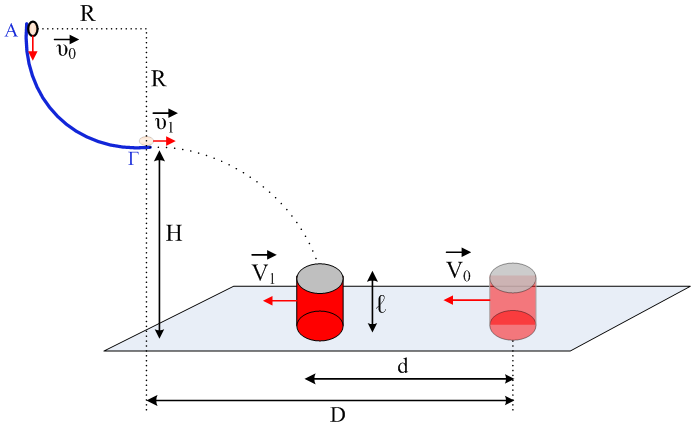
Σώμα μάζας m = 0,2 kg βάλλεται από την κορυφή τεταρτοκυκλίου με ταχύτητα μέτρου υ₀ = 5 m/s, που το κατώτερο του σημείο απέχει απόσταση H = 1 m από το οριζόντιο δάπεδο. Αφού εξέλθει από το τραχύ τεταρτοκύκλιο με οριζόντια ταχύτητα μέτρου υ₁ συναντά κουβά – μάζας Μ = 0,5 kg τον οποίο εκτοξεύσαμε από απόσταση D από την κατακόρυφο που περνά από το κατώτερο σημείο του τεταρτοκυκλίου – και μπαίνει μέσα σ’ αυτόν. Την στιγμή που συναντά την επιφάνεια του κουβά, έχοντας ταχύτητα μέτρου υ₂, σχηματίζει με τον ορίζοντα (η ταχύτητα) γωνία θ = 45^ο. Το ύψος του κουβά είναι ℓ = 20 cm, και η ταχύτητα εκείνη τη στιγμή έχει μέτρο V. Ο κουβάς παρουσιάζει με το δάπεδο τριβή, με συντελεστή τριβής μ = 0,2. Να βρείτε:

α. το μέτρο της ταχύτητας υ₁

β. την κάθετη δύναμη που ασκεί το τεταρτοκύκλιο στο σώμα μάζας m λίγο πριν το εγκαταλείψει

γ. την απώλεια της ενέργειας του σώματος μάζας m κατά την ολίσθηση του στο τεταρτοκύκλιο

δ. αν ο κουβάς έχει απώλεια ενέργειας κατά την κίνηση του στο οριζόντιο δάπεδο ίση με αυτή του σώματος μάζας m στο τεταρτοκύκλιο να βρείτε την απόσταση D

ε. την κινητική ενέργεια του κουβά την στιγμή που συναντά το σώμα μάζας m.

Δίνεται g = 10 m/s², η ακτίνα του τεταρτοκυκλίου R = 0,55 m και ότι η στιγμή εκτόξευσης του κουβά είναι η στιγμή που το σώμα μάζας m εγκαταλείπει το τεταρτοκύκλιο.