
Ένας δίσκος στρέφεται με το επίπεδό του κατακόρυφο, γύρω από σταθερό οριζόντιο άξονα ο οποίος περνά από το κέντρο του Ο, με σταθερή γωνιακή ταχύτητα ω, όπως στο σχήμα. Δυο μικρά σημειακά σώματα Σ1 και Σ2, της ίδιας μάζας, έχουν καρφωθεί στα σημεία Α και Β, όπου το Β βρίσκεται στο άκρο μιας ακτίνας R του δίσκου.
i) Να σχεδιαστούν, πάνω στο σχήμα, οι ταχύτητες και οι επιταχύνσεις των σωμάτων Σ1 και Σ2.
ii) Μεγαλύτερη επιτάχυνση (κατά μέτρο) έχει:
α) Το σώμα Σ1, β) Το σώμα Σ2, γ) Έχουν επιταχύνσεις του ίδιου μέτρου.
iii) Να σχεδιάστε επίσης, σε ένα νέο σχήμα, την κεντρομόλο δύναμη που ασκείται σε κάθε σώμα.
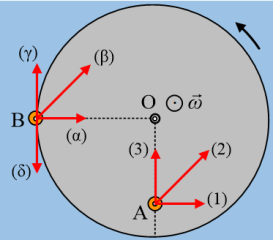

iv) Αν τη στιγμή που δείχνει το σχήμα, η ακτίνα R είναι οριζόντια και η r κατακόρυφη:
α) Ποιο από τα διανύσματα (1), (2), (3) παριστάνει την δύναμη F1 που ασκεί ο δίσκος στο σώμα Σ1;
β) Ποια η αντίστοιχη απάντηση για το διάνυσμα που παριστάνει την δύναμη F2που ασκεί στο σώμα Σ2 ο δίσκος;
v) Αν ω2=g/R, όπου g η επιτάχυνση της βαρύτητας και R η ακτίνα του δίσκου, να αποδείξετε ότι η δύναμη F2 σχηματίζει γωνία 45° με την κατακόρυφη διεύθυνση.

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου