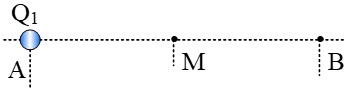 Ακίνητο σημειακό ηλεκτρικό φορτίο Q1 βρίσκεται στο σημείο Α και δημιουργεί γύρω του ηλεκτροστατικό πεδίο. Σε σημείο Μ ((ΑΜ) = r1) του πεδίου αυτού, το μέτρο της έντασης είναι Ε1Μ = 2∙107 N/C και η τιμή του δυναμικού είναι V1Μ = –6∙105 V.
Ακίνητο σημειακό ηλεκτρικό φορτίο Q1 βρίσκεται στο σημείο Α και δημιουργεί γύρω του ηλεκτροστατικό πεδίο. Σε σημείο Μ ((ΑΜ) = r1) του πεδίου αυτού, το μέτρο της έντασης είναι Ε1Μ = 2∙107 N/C και η τιμή του δυναμικού είναι V1Μ = –6∙105 V.
α. Να υπολογίσετε το φορτίο Q1 και κατόπιν να σχεδιάσετε το διάνυσμα της έντασης του ηλεκτροστατικού πεδίου στο σημείο Μ.
- Φέρουμε στο σημείο Β, σημειακό ηλεκτρικό φορτίο Q2 (Μ το μέσο της ΑΒ, (ΜΒ) = r2) με αποτέλεσμα το δυναμικό στο μέσο Μ να μηδενιστεί.
β. Να υπολογίσετε το φορτίο Q2 και να βρείτε την συνολική ένταση (η κατεύθυνση να φαίνεται στις απαντήσεις σας όχι πάνω στα θέματα) στο σημείο Μ.
- Σε κάποιο σημείο του χώρου (όπου υπάρχει το ηλεκτρικό πεδίο εξαιτίας των Q1, Q2) ένα σημειακό δοκιμαστικό φορτίο q έχει δυναμική ενέργεια UΚ = –2∙10–5 J,
γ. Να υπολογίσετε το απαιτούμενο έργο κατά τη μετακίνηση του φορτίου q από το σημείο Κ στο Μ.
δ. Το σημείο Κ θα μπορούσε να είναι σημείο της μεσοκαθέτου του ευθύγραμμου τμήματος ΑΒ; Εξηγήστε. (δεν χρειάζονται πράξεις).
Δίνεται η ηλεκτρική σταθερά k = 9∙109 N∙m2/C2.
Η συνέχεια εδώ.







 ΘΕΜΑ
Δ
ΘΕΜΑ
Δ





