Άλλο ένα test στην Επαγωγή. 2011

Ένας αγωγός ΑΓ μήκους ℓ=1m μάζας 0,2kg και αντίστασης r=0,5Ω, εκτοξεύεται κατακόρυφα με φορά προς τα πάνω, σε επαφή με  δύο κατακόρυφους στύλους, χωρίς αντίσταση, τα πάνω άκρα των οποίων συνδέονται μέσω αντιστάτη με αντίσταση R=1,5Ω. Ο αγωγός κινείται κάθετα στις δυναμικές γραμμές ενός οριζόντιου ομογενούς μαγνητικού πεδίου έντασης Β=0,5Τ, όπως στο σχήμα και  σε μια στιγμή t₁ έχει ταχύτητα υ=6m/s.

i) Για τη στιγμή αυτή:

α)  Να βρεθεί η ένταση του ρεύματος που διαρρέει τον αγωγό και η τάση V_ΑΓ.

β)  Να υπολογισθεί η επιτάχυνση του αγωγού.

γ)  Να βρεθεί η ισχύς της δύναμης Laplace. Τι ενεργειακή μετατροπή εκφράζει η ισχύς αυτή;

ii)  Να εξηγήστε γιατί ο αγωγός μετά από λίγο θα κινείται με φορά προς τα κάτω και να βρεθεί ο ρυθμός μεταβολής της κινητικής ενέργειας του αγωγού τη στιγμή που θα πέφτει με ταχύτητα μέτρου 10m/s. Πόση είναι τότε η τάση V_ΑΓ;

Δίνεται g=10m/s².

Μονάδες 3∙4+8=20

Ένα test στην Επαγωγή

Ένα τετράγωνο μεταλλικό πλαίσιο ΚΛΜΝ πλευράς 0,5m, μάζας 0,4kg και αντίστασης 2Ω, κινείται οριζόντια με την επίδραση μεταβλητής οριζόντιας δύναμης F και εισέρχεται σε ένα κατακόρυφο ομογενές μαγνητικό πεδίο έντασης Β=2Τ, όπως στο σχήμα. 

Σε μια στιγμή t₁, όπου μέσα στο πεδίο βρίσκεται το μισό πλαίσιο, η ταχύτητά του είναι υ₁=4m/s ενώ η δύναμη έχει μέτρο F=2,4Ν.

Α) Για τη στιγμή αυτή t₁:

i)  Να υπολογιστεί η μαγνητική ροή που διέρχεται από το πλαίσιο και να βρεθεί ο ρυθμός μεταβολής της μαγνητικής ροής.

ii)  Βρείτε την ένταση του ρεύματος που διαρρέει το πλαίσιο και την τάση V_ΚΛ.

iii) Ποιος ο ρυθμός μεταβολής της κινητικής ενέργειας του πλαισίου;

Β) Μετά από λίγο, τη στιγμή t₂, όλο το πλαίσιο είναι μέσα στο πεδίο κινούμενο με ταχύτητα υ₂=10m/s, ενώ  η δύναμη έχει μέτρο F=0,8Ν. Για τη στιγμή αυτή να βρεθούν:

i)       Η τάση V_ΚΛ.

ii)     Η επιτάχυνση του πλαισίου.

Ένα πλαίσιο σε δύο πεδία

Ένα τετράγωνο μεταλλικό πλαίσιο πλευράς α=1m και αντίστασης R=3Ω,  κινείται οριζόντια σε χώρο που υπάρχουν δύο κατακόρυφα ομογενή μαγνητικά πεδία, κάθετα στις δυναμικές γραμμές, όπως στο σχήμα, όπου Β₁=1Τ και Β₂=2Τ. Το πλαίσιο κινείται με σταθερή ταχύτητα υ=5m/s, με την επίδραση μιας οριζόντιας εξωτερικής δύναμης F.

Για τη θέση που φαίνεται στο σχήμα να βρεθούν:

i)  Η ένταση του ρεύματος που διαρρέει το πλαίσιο.

ii) Το μέτρο της εξωτερικής δύναμης F.

iii)  Οι τάσεις V_ΚΛ και V_ΝΜ.

Απάντηση:

Ερωτήσεις Ηλεκτρομαγνητισμού.

1)  Στο επίπεδο της σελίδας έχουμε ένα ορθογώνιο τρίγωνο ΚΛΜ. Από τις κορυφές Λ και Μ και κάθετα στο επίπεδο του τριγώνου διέρχονται δύο ευθύγραμμοι ρευματοφόροι αγωγοί που διαρρέονται από ρεύματα Ι₁=Ι₂, όπως στο σχήμα.

 

i)  Να σχεδιάστε την ένταση του μαγνητικού πεδίου στην κορυφή Κ.

ii) Πού είναι μεγαλύτερη η ένταση του πεδίου  στην κορυφή Κ ή στο μέσον O της ΛΜ;

2)  Σε οριζόντιο επίπεδο βρίσκεται ένας κυκλικός αγωγός που διαρρέεται από ρεύμα.

 i)   Να σχεδιάστε την ένταση του μαγνητικού πεδίου στα σημεία Ο, Α και Γ όπου Ο το κέντρο του κυκλικού αγωγού.

ii) Η ένταση του πεδίου στο σημείο Α είναι:

α) κατακόρυφη,   β) οριζόντια,   γ)  πλάγια.

iii) Για το μέτρο της έντασης στα σημεία Α και Γ ισχύει:

α) Β_Α<Β_Γ,                 β) Β_Α=Β_Γ,        γ) Β_Α>Β_Γ.

Απάντηση

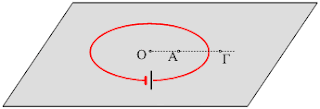
Επαγωγή και πηγή.

Ο α­γω­γός ΑΓ έ­χει μή­κος 1m μάζα 2kg και α­ντί­στα­ση 3Ω και αφήνεται να κινηθεί ό­πως στο σχή­μα υ­πό την ε­πί­δρα­ση της στα­θε­ρής δύ­να­μης F =20Ν. Αν Β=2Τ και η πηγή έχει ΗΕΔ Ε=20V και εσωτερική αντίσταση r=1Ω.

i)  Ποια η αρχική επιτάχυνση που αποκτά ο αγωγός;

ii)  Μετά από λίγο ο αγωγός έχει ταχύτητα 4m/s. Για τη στιγμή αυτή:

α)  Ποια η ένταση του ρεύματος που διαρρέει το κύκλωμα;

β) Βρείτε την ισχύ της δύναμης F, την ισχύ της δύναμης Laplace και τον ρυθμό με τον οποίο αυξάνεται η κινητική ενέργεια της ράβδου.

γ) Να βρείτε την ισχύ της γεννήτριας, την ισχύ της ΗΕΔ από επαγωγή και την ισχύ που μετατρέπεται σε θερμότητα στο κύκλωμα.

Να σχολιάστε τα αποτελέσματα.

Απάντηση

Μαγνητική Ροή και επαγωγή.

Αφήνουμε τον αγωγό KΛ μάζας 1kg, μήκους L=1m και αντίστασης r=1Ω για t=0 να κινηθεί κατακόρυφα, από την οριζόντια θέση ΑΓ, όπως στο σχήμα, όπου R=3Ω και Β=2Τ. Μετά από χρόνο t₁ ο αγωγός έχει κατέλθει κατά y=2m και έχει αποκτήσει ταχύτητα υ₁=5m/s.

i) Για τη στιγμή t₁, να βρεθούν:

 α)  Η μαγνητική ροή που διέρχεται από το σχηματιζόμενο πλαίσιο ΑΓΚΛ, καθώς και ο ρυθμός μεταβολής της ροής. Θεωρείστε ότι η κάθετη στο πλαίσιο έχει την κατεύθυνση των δυναμικών γραμμών.

β)   Η επιτάχυνση του αγωγού ΑΓ.

ii)  Πόση θερμότητα αναπτύχθηκε στο κύκλωμα από 0-t₁.

iii)  Υπολογίστε το συνολικό φορτίο που μετακινήθηκε στο κύκλωμα από 0-t₁.

Δίνεται:    g=10m/s².

Απάντηση:

Κινήσεις φορτισμένων σωματιδίων λόγω ηλεκτρικών αλληλεπιδράσεων

Α) Για όσο χρονικό διάστημα αλληλεπιδρούν:

1) Τα μέτρα των ηλεκτρικών δυνάμεων αλληλεπίδρασης είναι ίσα

2) Το μέτρο του ρυθμού μεταβολής της ταχύτητας του σωματιδίου α είναι κάθε στιγμή ίσο με το μέτρο του ρυθμού μεταβολής της ταχύτητας του πυρήνα ασβεστίου

3) Το μέτρο του ρυθμού μεταβολής της ταχύτητας του σωματιδίου α είναι κάθε στιγμή δεκαπλάσιο από το μέτρο του ρυθμού μεταβολής της ταχύτητας του πυρήνα ασβεστίου

4) Η ολική ορμή του συστήματος των σωματιδίων διατηρείται σταθερή , αφού οι δυνάμεις ηλεκτρικής αλληλεπίδρασης είναι εσωτερικές δυνάμεις του συστήματος, το δε μέτρο της είναι ίσο με p_ολ =9m_aυ_ο

5) Η ολική ορμή του συστήματος των σωματιδίων διατηρείται σταθερή , αφού οι δυνάμεις ηλεκτρικής αλληλεπίδρασης είναι συντηρητικές, το δε μέτρο της είναι ίσο με p_ολ =11m_aυ_ο

6) Η μηχανική ενέργεια του συστήματος των δύο σωματιδίων διατηρείται σταθερή, αφού οι
δυνάμεις ηλεκτρικής αλληλεπίδρασης είναι συντηρητικές και είναι ίση...........

Συνέχεια