Πληροφορίες από ένα διάγραμμα ταχύτητας.

 

Σε λείο οριζόντιο επίπεδο κινούνται ευθύγραμμα δυο ελαστικές σφαίρες Α και Β, με ίσες ακτίνες και κάποια στιγμή συγκρούονται κεντρικά. Στο διάγραμμα βλέπετε την μεταβολή της ταχύτητας της Α σφαίρας, σε συνάρτηση με το χρόνο.

i) Ποιο από τα παρακάτω σχήματα, δείχνει τις θέσεις και τις ταχύτητες των δύο σφαιρών πριν την κρούση;

 

ii) Ποιο από τα παρακάτω διαγράμματα θα μπορούσε να περιγράψει την ταχύτητα της Β  σφαίρας σε συνάρτηση με το χρόνο;

iii) Σχεδιάσαμε στο ίδιο διάγραμμα την ορμή κάθε σώματος σε συνάρτηση με το χρόνο. Ποιο από τα παρακάτω διαγράμματα πήραμε;

Να δικαιολογήσετε τις επιλογές σας

Απαντήσεις:

ή

Πληροφορίες από ένα διάγραμμα ταχύτητας.

Πληροφορίες από ένα διάγραμμα ταχύτητας.

Η ορμή και ο ρυθμός μεταβολής της ορμής.

Σε λείο οριζόντιο επίπεδο ηρεμεί ένα σώμα Α μάζας Μ=2kg. Ένα βλήμα μάζας m=0,1kg που κινείται οριζόντια με ταχύτητα υ₀= 100m/s, συγκρούεται με το σώμα Α, το διαπερνά σε χρόνο Δt=0,2s και εξέρχεται με ταχύτητα υ₁=40m/s.

i) Να υπολογιστεί η ταχύτητα του σώματος Α μετά την κρούση.

ii) Να βρεθεί  η μεταβολή της ορμής του βλήματος;

iii) Να υπολογιστεί η μέση δύναμη που δέχτηκε το βλήμα κατά το πέρασμά του μέσα από το σώμα Α, καθώς και ο μέσος ρυθμός μεταβολής της ορμής του σώματος Α στη διάρκεια της κρούσης.

Μια σφαίρα μάζας Μ=2kg είναι δεμένη στο άκρο νήματος μήκους ℓ=0,45m, το άλλο άκρο του οποίου είναι δεμένο στο ταβάνι. Φέρνουμε τη σφαίρα στη θέση Γ που δείχνει το σχήμα, όπου το νήμα είναι οριζόντιο και την αφήνουμε να κινηθεί.

iv) Να υπολογιστεί η ορμή και ο (στιγμιαίος) ρυθμός μεταβολής της ορμής της σφαίρας, τη στιγμή που το νήμα γίνεται κατακόρυφο.

Δίνεται g=10m/s².

Απάντηση:

ή

 Η ορμή και ο ρυθμός μεταβολής της ορμής.

 Η ορμή και ο ρυθμός μεταβολής της ορμής.

Η ορμή και οι μεταβολές της

Μια σφαίρα μάζας m=2kg κινείται σε λείο οριζόντιο επίπεδο, δεμένη στο άκρο νήματος μήκους ℓ=0,8m, διαγράφοντας κυκλική τροχιά κέντρου Ο, με γραμμική ταχύτητα σταθερού μέτρου υ=0,6m/s (το σχήμα σε κάτοψη).

i)  Να βρεθεί η ορμή και ο ρυθμός μεταβολής της ορμής (διεύθυνση, φορά και μέτρο) της σφαίρας στη θέση Α.

ii)  Σε πόσο χρόνο η σφαίρα θα φτάσει για πρώτη  φορά στη θέση Β, αντιδιαμετρική της θέσης Α; Να υπολογιστεί η μεταβολή της ορμής της σφαίρας στο παραπάνω χρονικό διάστημα.

iii) Μετά από λίγο η μπάλα φτάνει στη θέση Γ, όπου η ακτίνα ΟΓ είναι κάθετη στη διάμετρο ΑΒ. Να υπολογιστεί η μεταβολή της ορμής της σφαίρας μεταξύ των θέσεων Β και Γ.

iv) Να βρεθεί τέλος η μεταβολή της ορμής της σφαίρας, μεταξύ των θέσεων Γ και Δ, αν δίνεται για τη γωνία θ του σχήματος ημθ=0,6 και συνθ=0,8.

Απάντηση:

ή

Η ορμή και οι μεταβολές της

Η ορμή και οι μεταβολές της

Δυο υλικά σημεία σε ΟΚΚ.

Ένας δίσκος στρέφεται με το επίπεδό του κατακόρυφο, γύρω από σταθερό οριζόντιο άξονα ο οποίος περνά από το κέντρο του Ο, με σταθερή γωνιακή ταχύτητα ω, όπως στο σχήμα. Δυο μικρά σημειακά σώματα Σ₁ και Σ₂, της ίδιας μάζας, έχουν καρφωθεί στα σημεία Α και Β, όπου το Β βρίσκεται στο άκρο μιας ακτίνας R του δίσκου.

i)  Να σχεδιαστούν, πάνω στο σχήμα, οι ταχύτητες και οι επιταχύνσεις των σωμάτων Σ₁ και Σ₂.

ii) Μεγαλύτερη επιτάχυνση (κατά μέτρο) έχει:

α) Το σώμα Σ₁,   β) Το σώμα Σ₂,  γ) Έχουν επιταχύνσεις του ίδιου μέτρου.

iii) Να σχεδιάστε επίσης, σε ένα νέο σχήμα, την κεντρομόλο δύναμη που ασκείται σε κάθε σώμα.

 

iv) Αν τη στιγμή που δείχνει το σχήμα, η ακτίνα R είναι οριζόντια και η r κατακόρυφη:

α) Ποιο από τα  διανύσματα (1), (2), (3) παριστάνει την δύναμη F₁ που ασκεί ο δίσκος στο σώμα Σ₁;

β) Ποια η αντίστοιχη απάντηση για το διάνυσμα που παριστάνει την δύναμη F₂που ασκεί στο σώμα Σ₂ ο δίσκος;

v) Αν ω²=g/R, όπου g η επιτάχυνση της βαρύτητας και R η ακτίνα του δίσκου, να αποδείξετε ότι η δύναμη F₂ σχηματίζει γωνία 45° με την κατακόρυφη διεύθυνση.

Απάντηση:

ή

  Δυο υλικά σημεία σε ΟΚΚ.

  Δυο υλικά σημεία σε ΟΚΚ. 

Έργα και δυναμικές ενέργειες

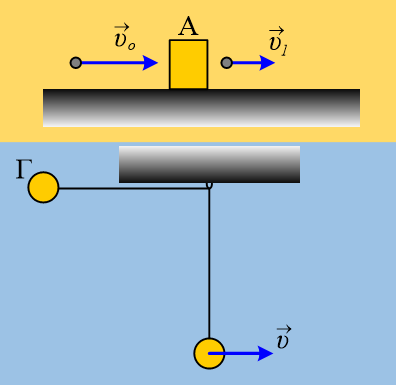
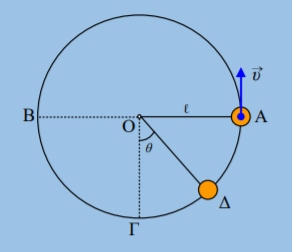
1) Μια σφαίρα κρέμεται στο άκρο νήματος, όπως στο σχήμα. Σε μια στιγμή ασκείται πάνω της μια σταθερή κατακόρυφη δύναμη μέτρου F=4Ν και την επιταχύνει μέχρι να φτάσει στη θέση Β, όπου (ΑΒ)=0,5m, όπου η δύναμη καταργείται.

i) Πόση είναι η δυναμική ενέργεια της σφαίρας στη θέση Α;

ii) Πόση ενέργεια μεταφέρθηκε στη σφαίρα, μέσω του έργου της δύναμης F;

iii) Η κινητική ενέργεια της σφαίρας στη θέση Β είναι:
                            α) Κ_Β< 0,2J,   β) Κ_Β= 0,2J,    γ) Κ_Β> 0,2J 

iv) Αν η σφαίρα σταματά την άνοδό της στη θέση Γ, να βρεθεί η μεταβολή της δυναμικής ενέργειας της σφαίρας μεταξύ των θέσεων Α και Γ.

v) Αν η σφαίρα έχει μάζα 1kg, να υπολογιστεί η ταχύτητα της σφαίρας τη στιγμή που επιστρέφει στην αρχική της θέση Α (πριν τεντωθεί το νήμα…)

2) Σε λείο μονωτικό οριζόντιο επίπεδο έχει στερεωθεί ακλόνητα ένα σημειακό φορτίο Q. Μια μικρή φορτισμένη σφαίρα συνδέεται με το φορτίο Q  με αβαρές και μονωτικό νήμα, ενώ φέρει φορτίο q₁. Σε μια στιγμή ασκείται πάνω της μια σταθερή οριζόντια δύναμη μέτρου F₁=2Ν, η οποία την επιταχύνει μέχρι να φτάσει στη θέση Β, όπου (ΑΒ)=0,2m, όπου η δύναμη καταργείται.

i) Πόση είναι η δυναμική ηλεκτρική ενέργεια της φορτισμένης σφαίρας στη θέση Α;

ii) Πόση ενέργεια μεταφέρθηκε στη σφαίρα, μέσω του έργου της δύναμης F;

iii) Η κινητική ενέργεια της σφαίρας στη θέση Β είναι:

α) Κ_Β< 0,4J,   β) Κ_Β= 0,4J,    γ) Κ_Β> 0,4J

iv) Αν η σφαίρα σταματά την κίνησή της στη θέση Γ, να βρεθεί η μεταβολή της δυναμικής ενέργειας της σφαίρας μεταξύ των θέσεων Α και Γ.

v) Αν η σφαίρα έχει μάζα 0,2kg, να υπολογιστεί η ταχύτητά της, τη στιγμή που επιστρέφει στην αρχική της θέση Α (πριν τεντωθεί το νήμα…).

Απάντηση:

ή

 Έργα και δυναμικές ενέργειες

 Έργα και δυναμικές ενέργειες