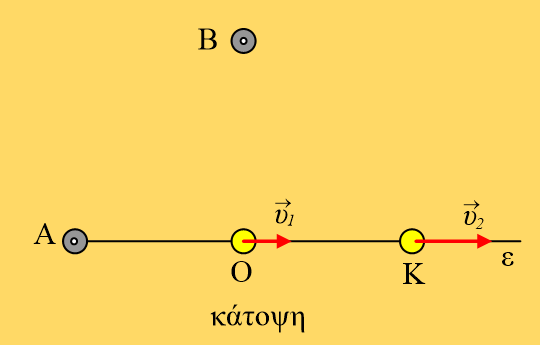
Μια σφαίρα μάζας m=2kg ηρεμεί στη θέση Α και θέλουμε να την μεταφέρουμε στη θέση Β, του διπλανού σχήματος, όταν μεταξύ των δύο σημείων παρεμβάλλεται ένα βουναλάκι ύψους h1=20m, ενώ η κατακόρυφη απόσταση των δύο σημείων είναι h2=15m. Τριβές δεν υπάρχουν.
i) Η μεταφορά μπορεί να γίνει με την επίδραση μιας μεταβλητής δύναμης F. Να υπολογιστεί το ελάχιστο έργο της δύναμης F, για την μεταφορά αυτή. Πόσο αυξήθηκε η μηχανική ενέργεια της σφαίρας κατά την παραπάνω μεταφορά;
ii) Εναλλακτικά μπορούμε να εκτοξεύσουμε τη σφαίρα, προσδίδοντάς της κατάλληλη αρχική ταχύτητα, η οποία θα της επιτρέψει να φτάσει στη θέση Β. Να υπολογιστεί η αρχική ταχύτητα εκτόξευσης, καθώς και η αύξηση της μηχανικής ενέργειας της σφαίρας, στην περίπτωση αυτή.

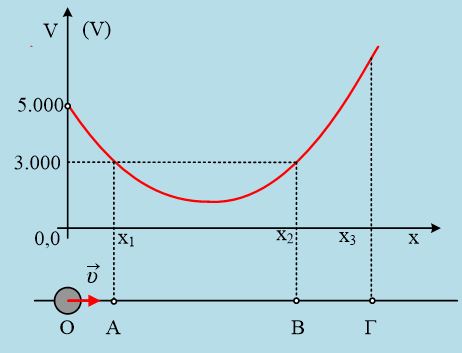
α) Ποια η ελάχιστη αρχική κινητική ενέργεια, που πρέπει να προσδώσουμε στο σώμα Σ για την μεταφορά του από τον πλανήτη Χ στον πλανήτη Υ;
β) Να βρεθεί η κινητική ενέργεια του σώματος Σ τη στιγμή που φτάνει στον πλανήτη Υ.